理解 PLONK（四）：算术约束与拷贝约束

回顾置换证明

上一节，我们讨论了如何让 Prover 证明两个长度为 $N$ 的向量 $a$ 与 $b$ 满足一个实现约定（公开）的置换关系 $σ (\cdot)$ ，即

$a_{i} = b_σ (i)$

基本思路是向 Verifier 要一个随机数 $β$ ，把两个「原始向量」和他们的「位置向量」进行合体，产生出两个新的向量，记为 $a^{'}$ 与 $b^{'}$

$a^{'}_i = a_{i} + β \cdot i, b_{i}^{'} = b_{i} + β \cdot σ (i)$

第二步是再向 Verifier 要一个随机数 $γ$ ，通过连乘的方法来编码 $a^{'}$ 和 $b^{'}$ 的 Multiset，记为 $A$ 和 $B$ ：

$A = \prod (a^{'} i + γ), B = \prod (b^{'} i + γ)$

第三步是让 Prover 证明 $A / B = 1$ ，即

$p ro d_{i} \frac{( a ^{'} _ i + γ )}{( b _{i}^{'} + γ )} = 1$

证明这个连乘，需要引入一个辅助向量 $z$ ，记录每次乘法运算的中间结果：

$z_{0} = 1, z i + 1 = z_{i} \cdot ( b ^{'} i + γ)$ (a′_i+γ)

由于 $z_{N} = \prod \frac{a ^{'} i + γ}{b ^{'} i + γ}$ =1，而且 $ω^{N} = 1$ ，因此我们可以用 $z (X)$ 来编码 $z$ ，从而把置换证明转换成关于 $z (X), a (X)$ 的关系证明。

最后 Verifier 发送挑战数 $ζ$ ，得到 $z (ζ), z (ω \cdot ζ), a (ζ), b (ζ)$ 然后检查它们之间的关系。

向量的拷贝约束

所谓拷贝约束 Copy Constraints，是说在一个向量中，我们希望能证明多个不同位置上的向量元素相等。我们先从一个简单例子开始：

$v ec a = (a_{0}, a_{1}, a_{2}, a_{3})$

假设为了让 Prover 证明 $a_{0} = a_{2}$ ，我们可以把 $a_{0}$ 与 $a_{2}$ 对调位置，这样形成一个「置换关系」，如果我们用 $(0, 1, 2, 3)$ 记录被置换向量的元素位置，那么我们把置换后的位置向量记为 $σ$ ，而 $a_s i g ma$ 为表示按照 $σ$ 置换后的向量

$s i g ma = (2, 1, 0, 3), a_s i g ma = (a_{2}, a_{1}, a_{0}, a_{3})$

显然，只要 Prover 可以证明置换前后的两个向量相等， $a = a_s i g ma$ ，那么我们就可以得出结论： $a_{0} = a_{2}$ 。

这个方法可以推广到证明一个向量中有多个元素相等。比如要证明 $a$ 中的前三个元素都相等，我们只需要构造一个置换，即针对这三个元素的循环右移：

$s i g ma = (2, 0, 1, 3), a_s i g ma = (a_{2}, a_{0}, a_{1}, a_{3})$

那么根据 $a = a_s i g ma$ 容易得出 $a_{0} = a_{1} = a_{2}$ 。

多个向量间的拷贝约束

对于 Plonk 协议，拷贝约束需要横跨 $W$ 表格的所有列，而协议要求 Prover 要针对每一列向量进行多项式编码。我们需要对置换证明进行扩展，从而支持横跨多个向量的元素等价。

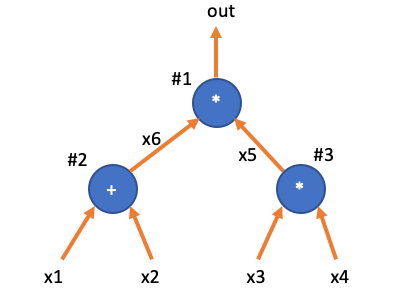
回忆比如针对上面电路的 $W$ 表格：

\begin{array}{c|c|c|c|} i & w_a & w_b & w_c \ \hline 0 & 0 & 0 & {\color{green}out} \ 1 & {\color{red}x_6} & {\color{blue}x_5} & {\color{green}out} \ 2 & x_1 & x_2 & {\color{red}x_6} \ 3 & x_3 & x_4 & {\color{blue}x_5} \ \end{array}

看上面的表格，我们要求 $w a, 1 = w c, 2$ ， $w b, 1 = w c, 3$ 且 $w c, 0 = w c, 1$ 。

支持跨向量置换的直接方案是引入多个对应的置换向量，比如上表的三列向量用三个置换向量统一进行位置编码：

\begin{array}{c|c|c|c|} i & id_{a,i} & id_{b,i} & id_{c,i} \ \hline 0 & 0 & 4 & {\color{green}8} \ 1 & {\color{red}1} & {\color{blue}5} & {\color{green}9} \ 2 & 2 & 6 & {\color{red}10} \ 3 & 3 & 7 & {\color{blue}11} \ \end{array}

置换后的向量为 $σ_{a}, σ_{b}, σ_{c}$ ：

\begin{array}{c|c|c|c|} i & \sigma_{a,i} & \sigma_{b,i} & \sigma_{c,i} \ \hline 0 & 0 & 4 & {\color{green}9} \ 1 & {\color{red}10} & {\color{blue}11} & {\color{green}8} \ 2 & 2 & 6 & {\color{red}1} \ 3 & 3 & 7 & {\color{blue}5} \ \end{array}

Prover 用一个随机数 $β$ （Verifier 提供）来合并 $(w a, i d_{a})$ ， $(w$ b,idb)， $(w c, i d_{c})$ ，还有置换后的向量： $(w$ a′,σa) ， $(w b^{'}, σ_{b})$ ， $(w$ c′,σc) 。然后再通过一个随机数 $γ$ （Verifier 提供）和连乘来得到 $W$ 和 $W^{'}$ 的 Multisets， $f_{i}$ 与 $g_{i}$

\begin{split} f_i &= (w_{a,i}+\beta\cdot id_{a,i}+\gamma)(w_{b,i}+\beta\cdot id_{b,i}+\gamma)(w_{c,i}+\beta\cdot id_{c,i}+\gamma) \ g_i &= (w’{a,i}+\beta\cdot \sigma{a,i}+\gamma)(w’{b,i}+\beta\cdot \sigma{b,i}+\gamma)(w’{c,i}+\beta\cdot \sigma{c,i}+\gamma) \end{split}

又因为拷贝约束要求置换后的向量与原始向量相等，因此 $w_{a} = w^{'}_a$ ， $w_{b} = w_{b}^{'}$ ， $w_{c} = w_{c}^{'}$ 。

如果我们用多项式对 $w a, w b, w c, i d a, i d b, i d$ c,σa,σb,σc 编码，得到 $w_{a} (X), w_{b} (X), w_{c} (X), i d_{a} (X), i d_{b} (X), i d_{c} (X), σ_{a} (X), σ_{b} (X), σ_{c} (X)$ ，于是 $f (X)$ ， $g (X)$ 满足下面的约束关系：

\begin{split} f(X)&=\Big(w_a(X)+\beta\cdot S_{id_a}(X)+\gamma\Big)\Big(w_b(X)+\beta\cdot S_{id_b}(X)+\gamma\Big)\Big(w_c(X)+\beta\cdot S_{id_c}(X)+\gamma\Big)\ g(X)&=\Big(w_a(X)+\beta\cdot S_{\sigma_a}(X)+\gamma\Big)\Big(w_b(X)+\beta\cdot S_{\sigma_b}(X)+\gamma\Big)\Big(w_c(X)+\beta\cdot S_{\sigma_c}(X)+\gamma\Big)\ \end{split}

如果两个 Multiset 相等 $f_{i} = g_{i}$ ，那么下面的等式成立：

$p ro d X \in H f (X) = \prod X \in H g (X)$

上面的等式稍加变形，可得

$p ro d_X \in H \frac{f ( X )}{g ( X )} = 1$

我们进一步构造一个辅助的累加器向量 $z$ ，表示连乘计算的一系列中间过程

$z_{0} = 1, z_i + 1 = z_{i} \cdot \frac{f _{i}}{g _{i}}$

其中 $z_{0}$ 的初始值为 $1$ ，Prover 按照下表计算出 $z$ ：

\begin{array}{|c|c|c|} i & H_i & z_i\ \hline 0 & \omega^0=1 & 1\ 1 & \omega^1 & 1\cdot \frac{f_0}{g_0}\ 2 & \omega^2 & \frac{f_0}{g_0}\cdot \frac{f_1}{g_1}\ 3 & \omega^3 & \frac{f_0f_1}{g_0g_1}\cdot \frac{f_2}{g_2}\ \vdots & & \vdots\ N-1 & \omega^{N-1} & \frac{f_0f_1\cdots f_{N-3}}{g_0g_1\cdots g_{N-3}}\cdot \frac{f_{N-2}}{g_{N-2}} \ N & \omega^{N}=1 & \frac{f_0f_1\cdots f_{N-1}}{g_0g_1\cdots g_{N-1}} = 1 \end{array}

如果 $f$ 能与 $g$ 连乘等价的话，那么最后一行 $z_N$ 正好等于 $1$ ，即

$z_N = z_{0} = 1$

而又因为 $ω^{N} = 1$ 。这恰好使我们可以把 $(z_{0}, z_{1}, z_{2}, \dots, z N - 1)$ 完整地编码在乘法子群 $H$ 上。因此如果它满足下面两个多项式约束，我们就能根据数学归纳法得出 $z$ N=1，这是我们最终想要的「拷贝约束」：

$z (ω^{0}) = 1$

$z (ω \cdot X) g (X) = z (X) f (X)$

置换关系 $σ$

在构造拷贝约束前，置换关系 $σ$ 需要提前公开共识。表格 $W$ 含有所有算术门的输入输出，但是并没有描述门和门之间是否通过引线相连，而置换关系 $σ$ 实际上正是补充描述了哪些算术门之间的连接关系。

因此，对于一个处于「空白态」的电路，通过 $(Q, σ)$ 两个表格描述，其中 $Q$ 由选择子向量构成，而 $σ$ 则由「置换向量」构成。

下面是 $Q$ 表格

\begin{array}{c|c|c|c|} i & q_L & q_R & q_M & q_C & q_O \ \hline 0 & 0 & 0 & 0 & 99 & 1 \ 1 & 0 & 0 & 1 & 0 & 1 \ 2 & 1 & 1 & 0 & 0 & 1 \ 3 & 0 & 0 & 1 & 0 & 1 \ \end{array}

下面是 $S$ 表格，描述了哪些位置做了置换

\begin{array}{c|c|c|c|} i & \sigma_{a,i} & \sigma_{b,i} & \sigma_{c,i} \ \hline 0 & 0 & 4 & [9] \ 1 & \boxed{10} & \underline{11} & [8] \ 2 & 2 & 6 & \boxed{1} \ 3 & 3 & 7 & \underline{5} \ \end{array}

处理 Public Inputs

假如在上面给出的小电路中，要证明存在一个 Assignment，使得 out 的输入为一个特定的公开值，比如 $o u t = 99$ 。最简单的办法是使用 $Q$ 表中的 $q_{C}$ 列，并增加一行约束，使得 $q_{L} = q_{R} = q_{M} = 0$ ，因此满足下面等式

$q_{C} (X) - q_{O} (X) w_{c} (X) = 0$

但这个方案的问题是：这些公开值输入输出值被固定成了常数，如果公开值变化，那么 $q_{C} (X)$ 多项式需要重新计算。如果整体上 $W$ 表格的行数比较大，那么这个重新计算过程会带来很多的性能损失。

能否在表格中引入参数，以区分电路中的常数列？并且要求参数的变化并不影响其它电路的部分？这就需要再引入一个新的列，专门存放公开参数，记为 $ϕ$ ，因此，算术约束会变为：

$q_{L} (X) w_{a} (X) + q_{R} (X) w_{b} (X) + q_{M} (X) w_{a} (X) w_{b} (X) - q_{O} (X) w_{c} (X) + q_{C} (X) + ϕ (X) = 0$

我们还可以通过修改拷贝约束的方式引入公开参数。

[!TODO]

位置向量的优化

我们上面在构造三个 $σ$ 向量时，直接采用的自然数 $(0, 1, 2, \dots)$ ，这样在协议开始前，Verifier 需要构造 3 个多项式 $S i d_{a} (X), S i d_{b} (X), S i d_{c} (X)$ ，并且在协议最后一步查询 Oracle，获得三个多项式在挑战点 $X = ζ$ 处的取值 $(S$ ida(ζ),Sidb(ζ),Sidc(ζ)) 。

思考一下， $σ$ 向量只需要用一些互不相等的值来标记置换即可，不一定要采用递增的自然数。如果我们采用 $H = (1, ω, ω^{2}, \dots)$ 的话，那么多项式 $i d_{a} (X)$ 会被大大简化：

\begin{split} \vec{id}_a &= (1,\omega,\omega^2,\omega^3)\ \vec{id}_b &= (k_1,k_1\omega,k_1\omega^2,k_1\omega^3)\ \vec{id}_c &= (k_2,k_2\omega,k_2\omega^2,k_2\omega^3)\ \end{split}

其中 $k_{i}$ 为互相不等的二次非剩余。

$i d_{a} (X) = X, i d_{b} (X) = k_{1} \cdot X, i d_{a} (X) = k_{2} \cdot X$

这样一来，这三个多项式被大大简化，它们在 $X = ζ$ 处的计算轻而易举，可以直接由 Verifier 完成。

这个小优化手段最早由 Vitalik 提出。采用 $k_{1}$ 和 $k_{2}$ 是为了产生 $(1, ω, ω^{2}, ω^{3})$ 的陪集（Coset），并保证 Coset 之间没有任何交集。我们前面提到 $H = (1, ω, ω^{2}, ω^{3})$ 是 $F$ 的乘法子群，如果 $H_{1} = k_{1} H$ 和 $H_{2} = k_{2} H$ 存在交集，那么 $H_{1} = H_{2}$ 。这个论断可以简单证明如下：如果它们存在交集，那么 $k_{1} ω^{i} = k_{2} ω^{j}$ ，于是 $k_{1} = k_{2} \cdot ω^{j - i}$ ，又因为 $ω^{j - i} \in H$ ，那么 $k_{1} \in H_{2}$ ，那么 \forall i\in[N]. k_1\cdot \omega^i\in H_2，那么 $H_{1} \subset H_{2}$ ，同理可得 $H_{2} \subset H_{1}$ ，于是 $H_{1} = H_{2}$ 。

如果 $σ$ 的列数更多，那么我们需要选择多个 $k_{1}, k_{2}, k_{3}, \dots$ 且 $(k_{i} / k_{j})^{N} \neq = 1$ 来产生不相交的 Coset。一种最直接的办法是采用 $k_{1}, k_{2}, k_{3}, \dots = g^{1}, g^{2}, g^{3}, \dots$ ，其中 $g$ 为乘法子群 $T$ 的生成元， |T|*2^\lambda=p-1。

协议框架

预处理：Prover 和 Verifier 构造 [q_L(X)]， [q_R(X)]， [q_O(X)]， [q_M(X)]， [q_C(X)]， [{\sigma_a}(X)]， [{\sigma_b}(X)]， [{\sigma_c}(X)]

第一步：Prover 针对 $W$ 表格的每一列，构造 [w_a(X)]， [w_b(X)]， [w_c(X)]， $ϕ (X)$ 使得

$q_{L} (X) w_{a} (X) + q_{R} (X) w_{b} (X) + q_{M} (X) w_{a} (X) w_{b} (X) - q_{O} (X) w_{c} (X) + q_{C} (X) + ϕ (X) = 0$

第二步： Verifier 发送随机数 $β$ 与 $γ$ ；

第三步：Prover 构造 [z(X)]，使得

\begin{split} L_0(X)(z(X)-1) &= 0 \ z(\omega\cdot X)g(X) - z(X)f(X) &=0 \end{split}

第四步：Verifier 发送随机挑战数 $α$ ；

第五步：Prover 计算 $h (X)$ ，并构造商多项式 [t(X)]

\begin{split} h(X) = &\ q_L(X)w_a(X)+q_R(X)w_b(X)+ q_M(X)w_a(X)w_b(X) - q_O(X)w_c(X)+q_C(X) + \phi(X) \ & + \alpha(z(\omega X)\cdot g(X)-z(X)\cdot f(X)) + \alpha^2(L_0(X)\cdot(z(X)-1)) \end{split}

其中

\begin{split} f(X)&=\Big(w_a(X)+\beta\cdot {id_a}(X)+\gamma\Big)\Big(w_b(X)+\beta\cdot {id_b}(X)+\gamma\Big)\Big(w_c(X)+\beta\cdot {id_c}(X)+\gamma\Big)\ g(X)&=\Big(w_a(X)+\beta\cdot {\sigma_a}(X)+\gamma\Big)\Big(w_b(X)+\beta\cdot {\sigma_b}(X)+\gamma\Big)\Big(w_c(X)+\beta\cdot {\sigma_c}(X)+\gamma\Big)\ \end{split}

其中商多项式 $t (X) = \frac{h ( X )}{z _{H} ( X )}$ ；

第六步：Verifier 发送随机挑战数 $ζ$ ，查询上述的所有 Oracle，得到

$\overset{w}{ˉ} a = w_{a} (ζ)$ ， $\overset{w}{ˉ}$ b=wb(ζ)， $\overset{w}{ˉ}_c = w_{c} (ζ)$
$\overset{q}{ˉ} L = q_{L} (ζ)$ ， $\overset{q}{ˉ}$ R=qR(ζ)， $\overset{q}{ˉ} M = q_{M} (ζ)$ ， $\overset{q}{ˉ}$ O=qO(ζ)， $\overset{q}{ˉ}_C = q_{C} (ζ)$
$\overset{σ}{ˉ} a = σ_{a} (ζ)$ ， $\overset{σ}{ˉ}$ b=σb(ζ)， $\overset{σ}{ˉ}_c = σ_{c} (ζ)$
$\overset{z}{ˉ}_{(ω \cdot ζ)} = z (ω \cdot ζ)$ ， $\overset{z}{ˉ}_{(ζ)} = z (ζ)$
$\overset{ˉ}{t} = t (ζ)$

Verifier 还要自行计算

$\overset{ˉ}{f} (ζ) = (\overset{w}{ˉ} a +$ β⋅ζ+γ)(wˉb+β⋅k1⋅ζ+γ)(wˉc+β⋅k2⋅ζ+γ)
$\overset{g}{ˉ} (ζ) = (\overset{w}{ˉ} a +$ β⋅σˉ1+γ)(wˉb+β⋅σˉ2+γ)(wˉc+β⋅σˉ_3+γ)
$L_{0} (ζ)$
$z_{H} (ζ)$
$ϕ (ζ)$

验证步：

\begin{split} & \bar{q}_L\bar{w}_a+\bar{q}_R\bar{w}_b+ \bar{q}_M\bar{w}_a\bar{w}b - \bar{q}O\bar{w}c+\bar{q}C + \phi(\zeta) \ & \qquad \qquad + \alpha(\bar{z}{(\omega\cdot\zeta)}\cdot \bar{g}_{(\zeta)}-\bar{z}{(\zeta)}\cdot \bar{f}{(\zeta)})+ \alpha^2(L_0(\zeta)\cdot(\bar{z}{(\zeta)}-1))\overset{?}{=}\bar{t}\cdot z_H(\zeta) \end{split}

ZKPunk's ZKPedia