理解 PLONK(一):Plonkish Arithmetization
算术化是指把计算转换成数学对象,然后进行零知识证明。 Plonkish 算术化是 Plonk 证明系统特有的算术化方法,在 Plonkish 出现之前,主流的电路表达形式为 R1CS,被 Pinocchio,Groth16,Bulletproofs 等广泛采用。2019 年 Plonk 方案提出了一种看似复古的电路编码方式,但由于 Plonk 方案将多项式的编码应用到了极致,它不再局限于算术电路中的「加法门」和「乘法门」,而是可以支持更灵活的「自定义门」与「查表门」。
我们先回顾一下 R1CS 的电路编码,也是相关介绍最多的算术化方案。然后我们对比引入 Plonkish 编码。
算术电路与 R1CS 算术化
一个算术电路包含若干个乘法门与加法门。每一个门都有「两个输入」引脚和一个「输出」引脚,任何一个输出引脚可以被接驳到多个门的输入引脚上。
先看一个非常简单的算术电路:
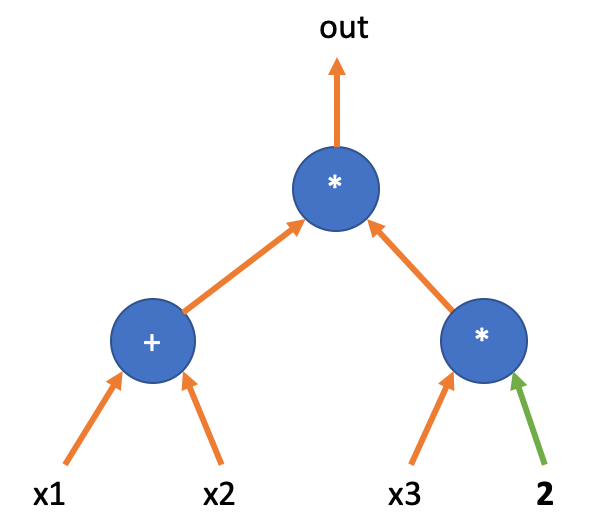
这个电路表示了这样的一个计算:
电路中有4个变量,其中三个变量为输入变量 ,一个输出变量 ,其中还有一个输入为常数,其值为 。
一个电路有两种状态:「空白态」和「运算态」。当输入变量没有具体值的时候,电路处于「空白态」,这时我们只能描述电路引线之间的关系,即电路的结构拓扑。
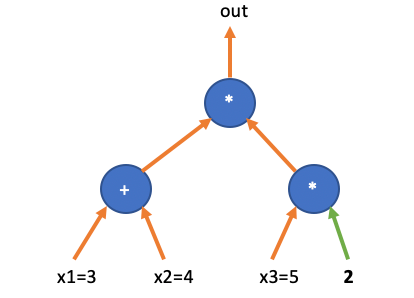
接下来的问题是,我们要先编码电路的「空白态」,即编码各个门的位置,和他们之间引线连接关系。
R1CS 是通过图中的乘法门为中心,用三个「选择子」矩阵来「选择」乘法门的「左输入」、「右输入」、「输出」都分别连接了那些变量。
我们先看看图中最上面的乘法门的左输入,可以用下面的表格来描述:
这个表格只有一行,因此我们可以用一个向量 来代替,表示乘法门的左输入连接了两个变量, 和 。记住,所有的加法门都会被展开成多个变量的相加(或线性组合)。
再看看其右输入,连接了一个变量 和一个常数值,等价于连接了 的两倍,那么右输入的选择子矩阵可以记为
这里同样可以用一个行向量 来表示,其中的 即为上图中电路的常数引线。
最后乘法门的输出按照上面的方法可以描述为 ,即输出变量为 :
有了三个向量 ,我们可以通过一个「内积」等式来约束电路的运算:
这个等式化简之后正好可以得到:
如果我们把这几个变量换成赋值向量 ,那么电路的运算可以通过「内积」等式来验证:
而一个错误的赋值向量,比如 ,则不满足「内积等式」:
左边运算结果为 ,右边运算结果为 。当然,我们可以验证 也是一组合法(满足电路约束)的赋值。
并不是任何一个电路都存在赋值向量。凡是存在合法的赋值向量的电路,被称为可被满足的电路。判断一个电路是否可被满足,是一个 NP-Complete 问题,也是一个 NP 困难问题。
这里例子中的两个乘法门并不相同,上面的乘法门是左右输入中都含有变量,而下面的乘法门只有一边的输入为变量,另一边为常数。对于后者这类「常数乘法门」,后续我们也把他们看作为特殊的「加法门」,如下图所示,左边电路右下的乘法门等价于右边电路的右下加法门。
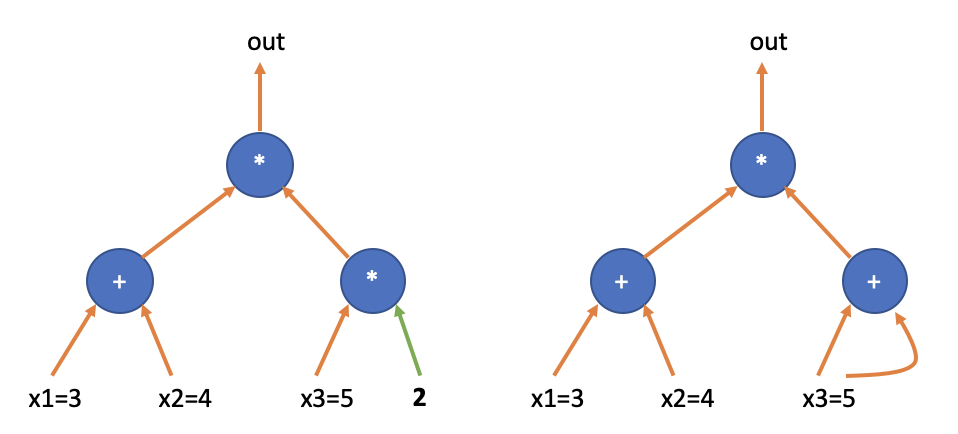
那么如果一个电路含有两个以上的乘法门,我们就不能用 三个向量之间的内积关系来表示运算,而需要构造「三个矩阵」的运算关系。
多个乘法门
比如下图所示电路,有两个乘法门,他们的左右输入都涉及到变量。
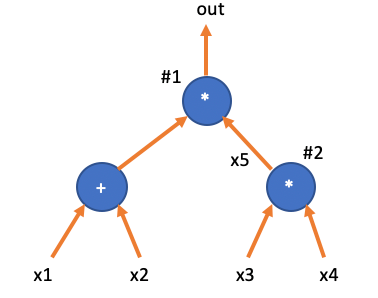
这个电路表示了这样的一个计算:
我们以乘法门为基准,对电路进行编码。第一步将电路中的乘法门依次编号(无所谓编码顺序,只要前后保持一致)。图中的两个乘法门编码为 #1 与 #2。
然后我们需要为每一个乘法门的中间值引线也给出变量名:比如四个输入变量被记为 ,其中 为第二个乘法门的输出,同时作为第一个乘法门的右输入。而 为第一个乘法门的输出。于是我们可以得到一个关于变量名的向量:
该电路的「空白态」可以用下面的三个矩阵来编码:
其中 为乘法门的数量,而 大致为引线的数量。每一个矩阵的第 行「选择」了第 个乘法门的输入输出变量。比如我们定义电路的左输入矩阵 :
其中第一个乘法门的左输入为 , 第二个乘法门的左输入为 。右输入矩阵 定义为:
其中1号门的右输入为 ,第二个乘法门的右输入为 。最后定义输出矩阵 :
我们把所有的引线赋值看作为一个向量: (这里用字母 ,取自 Assignments 首字母)
在上面的例子中,「赋值向量」为
于是我们可以轻易地检验下面的等式
其中符号 为 Hadamard Product,表示「按位乘法」。展开上面的按位乘法等式,我们可以得到这个电路的运算过程:
请注意,通常「赋值向量」中需要一个固定赋值为 的变量,这是为了处理加法门中的常量输入。
优缺点
由于 R1CS 编码以乘法门为中心,于是电路中的加法门并不会增加 矩阵的行数,因而对 Prover 的性能影响不大。R1CS 电路的编码清晰简单,利于在其上构造各种 SNARK 方案。
在 2019 年 Plonk 论文中的编码方案同时需要编码加法门与乘法门,看起来因此会增加约束的数量,降低 Proving 性能。但 Plonk 团队随后陆续引入了除乘法与加法外的运算门,比如实现范围检查的门,实现异或运算的门等等。不仅如此,Plonk 支持任何其输入输出满足多项式关系的门,即 Custom Gate,还有适用于实现 RAM 的状态转换门等,随着查表门的提出,Plonk 方案逐步成为许多应用的首选方案,其编码方式也有了一个专门的名词:Plonkish。
Plonkish 算术门
回看下例子电路,我们把三个门全都编号, ,同时把加法门的输出值也标记为变量 。
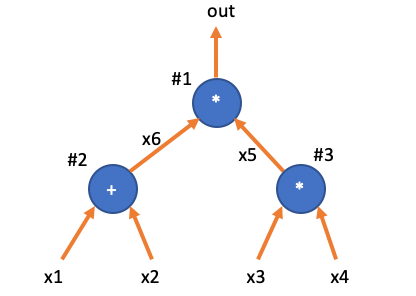
显然,上面的电路满足三个约束:
我们定义一个矩阵 来表示约束( 为算术门的数量):
为了区分加法和乘法,我们再定一个向量 来表示运算符
于是我们可以通过下面的等式来表示三个约束:
如果把上面的等式代入并展开,我们可以得到下面的约束等式:
化简后得:
这正好是三个算术门的计算约束。
总结下,Plonkish 需要一个矩阵 来描述电路空白态,而所有的赋值则写入了 矩阵。对于 Prover 和 Verifier 的交换协议, 是 Prover 的 witness,属于秘密知识,对 Verifier 保密, 矩阵代表了一个实现双方约定共识的电路描述。
不过仅仅有 矩阵是不足以精确描述上面的例子电路。
复制约束
比较下面两个电路,它们的 矩阵完全相同,但它们却完全不同。
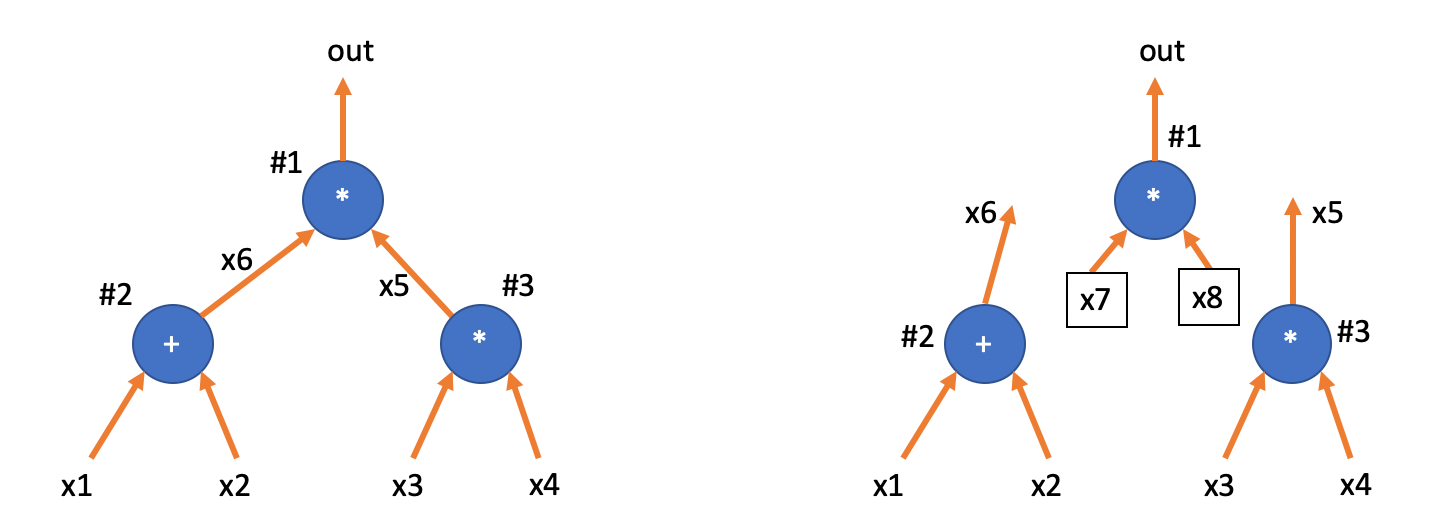
两个电路的区别在于 是否被接入了 #1 号门。如果让 Prover 直接把电路赋值填入 表格,一个「诚实的」Prover 会在 和 两个位置填上相同的值;而一个「恶意的」Prover 完全可以填上不同的值。如果恶意 Prover 在 和 也填入不同的值,那么实际上 Prover 证明的是上图右边的电路,而非是和 Verifier 共识过的电路(左边)。
我们需要增加新的约束,强制要求右边电路图中 和 。这等价于我们要求 Prover 把同一个变量填入表格多个位置时,必须填入相等的值。
这就需要一类新的约束——「拷贝约束」,即 Copy Constraint。Plonk 采用「置换证明」保证 表格中多个位置上的值满足拷贝关系。我们继续用上面这个电路图的案例来说明其基本思路:
设想我们把 表格中的所有位置索引排成一个向量:
然后把应该相等的两个位置互换,比如上图中要求 和 。于是我们得到了下面的位置向量:
然后我们要求 Prover 证明: 表格按照上面的置换之后,仍然等于自身。置换前后的相等性可以保证 Prover 无法作弊。
再来一个例子,当约束一个向量中有三个(或多个)位置上的值必须相同时,只需要把这三个(或多个)位置的值进行循环移位(左移位或者右移位),然后证明移位后的向量与原向量相等即可。比如:
如果要证明 ,那么只需要证明:
在经过置换的向量 中, 依次右移交换,即 放到了原来 的位置,而 放到了 的位置, 则放到了 的位置。
如果 ,那么 和 所有对应位置上的值都应该相等,可得: , , ,即 。这个方法可以适用于任意数量的等价关系。(后续证明两个向量相等的方法请见下章)
那么如何描述电路赋值表格中的交换呢?我们只需要记录 向量即可,当然 向量也可以写成表格的形式:
加上 ,空白电路可以描述为 ,电路的赋值为
再比较
R1CS 的 表格的宽度与引线的数量有关,行数跟乘法门数量有关。这个构造相当于把算术电路看成是仅有乘法门构成,但每个门有多个输入引脚(最多为所有引线的数量)。而 Plonkish 则是同等对待加法门与乘法门,并且因为输入引脚只有两个, 所以 表格的宽度固定,仅有三列(如果要支持高级的计算门,表格可以扩展到更多列)。这一特性是 Plonk 可以利用 Permutation Argument 实现拷贝约束的前提。
…, and thus our linear contraints are just wiring constraints that can be reduced to a permutation check.
按照 Plonk 论文的统计,一般情况下,算术电路中加法门的数量是乘法门的两倍。如果这样看来, 表格的行数会三倍于 R1CS 的矩阵。但这个让步会带来更多的算术化灵活度。
电路验证协议框架
有了电路空白结构的描述和赋值,我们可以大致描述下 Plonk 的协议框架。
首先 Prover 和 Verifier 会对一个共同的电路进行共识, 。 假设电路的公开输出为 ,而 为秘密输入。
Prover 填写 矩阵(Verifier 不可见):
其中增加的第四行是为了增加一个额外的算术约束: ,把 值显示地表示在 矩阵中。
相应的那么 Prover 和 Verifier 共识的 矩阵为
其中第四行约束,保证 ,可以把 代入下面的算术约束,可得 ,即 。
为了保证第一行的 也必须为 ,这就需要在 矩阵中添加额外的一条拷贝约束:让 变量的位置 与 第四行的输出 交换对调:
如果 Prover 是诚实的,那么对于 ,下面的算术约束等式成立:
验证协议的大概思路如下:
协议开始:Prover 如实填写 表格,然后把 表格的每一列进行编码,并进行多项式编码,并把编码后的结果发送给 Verifier
协议验证阶段:Verifier 与 Prover 通过进一步的交互,验证下面的等式是否成立:
当然这个验证还不够,还要验证 与 之间的关系。还有,Verifier 如何通过多项式来验证电路的运算,请看后续章节。
参考文献
- [BG12] Bayer, Stephanie, and Jens Groth. “Efficient zero-knowledge argument for correctness of a shuffle.” Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Berlin, Heidelberg, 2012.
- [GWC19] Ariel Gabizon, Zachary J. Williamson, and Oana Ciobotaru. “Plonk: Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge.” Cryptology ePrint Archive (2019).