Lattice基础
作者简介:Xor0v0,硕士在读,零知识证明小白,目前在做一些circom开发和zk审计,密码学爱好者,打过一些web2/3 CTF,最近对zkHACK产生兴趣。欢迎各位大佬一起交流学习。
Lattice是现代密码学非常重要的一部分,它也可以被用于构造零知识证明方案,比如这篇Lattice-Based zk-SNARKs from Square Span Programs。
我们知道密码学的底层依赖于一些数学难题,基于Lattice的密码学的底层当然依赖于一些Lattice的的数学难题,这些数学难题在本篇最后都会提及。格密码学被认为是一种后量子安全的密码学。
之所以想出这一系列,不是说基于Lattice的ZKP方案有多好或者多有前景。纯粹是一个密码学爱好者的个人分享,这是一个非常有意思的领域,另外如果有兴趣参加web2/web3 CTF、密码学竞赛或者ZK Puzzle的同学,这一块知识拼图也是必不可少的。BTW,了解这个领域需要大家拥有线性代数基础。
总之,我会在这一系列中跟大家一起学习lattice的知识,分享我在Web3 CTF或者ZK Puzzle中遇到的可以使用到lattice的解法【第二篇LLL算法应该就有题分享】。
希望大家各有所获!!
参考文献:最经典最地道的 Regev 讲义(源于它,但不仅仅是它),需要注意的是,这些讲义中通篇使用列向量表示矩阵,而非常规的行向量,这对于数学工作者也许不是什么大毛病,但是初学者一定要注意分辨,因为这样的矩阵使得整数线性组合向量在乘法的右边。
强力推荐大家看原文,如果觉得英文不好理解,可以再看这里有没有答案。
1. 什么是格Lattice?
格Lattice,顾名思义,就是一个个格子。严格来讲,格是一个数学对象,它的数学定义是:格Lattice由n维空间中具有周期结构的点集构成。【划重点:Lattice是空间内的离散点集】下图展示了一个二维实数空间的格点:

18世纪的大数学家们如Lagrange, Gauss 和后来的Minkowski,都研究过格。近年来,格被计算机科学领域所关注,被用于作为一种算法工具去解决各种问题,在密码学和密码分析中也有大量运用,并且这些构造出来的格从计算复杂性角度上讲拥有着独特的性质。
对于一个格,更正式的定义是:在m维实数空间,给定n个线性无关的m维向量 ,由这些向量定义的格就是:
说明:如果没有特别说明,粗体字母表示向量。
线性无关向量:给定一组向量 ,如果存在一组不全为零的系数 ,使得下面的等式成立:
则称这组向量是线性无关的。线性无关表示每一个元素都是相互独立,而没有冗余信息。
我们把这组线性无关向量称为格基(Basis of the lattice)。等价地,我们可以把这组向量按列展开,于是就得到它们的矩阵表示B,有:
我们定义格的秩(rank of lattice)为n,格的维度(dimension)为m。如果 ,那么则称这个格为满秩格(full-rank lattice)。如果没有特殊说明,本系列文章讲只讨论满秩格,因为其他情况并没有实质的差异。下面给出几个格的例子:
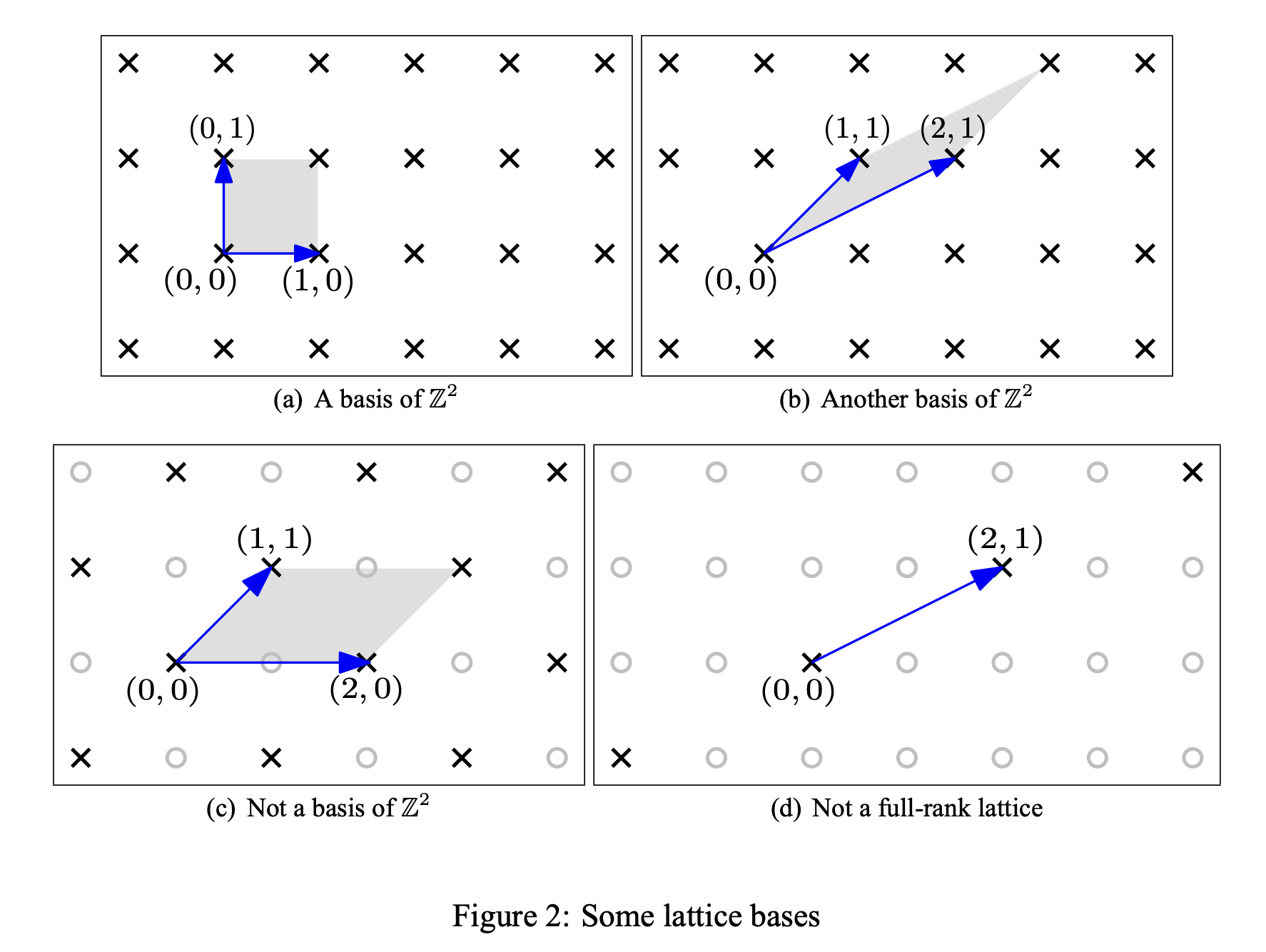
特别是: 是一个1维的满秩格。注意,一个维度空间的格基不唯一。
下面介绍两个概念:张成空间Span和基础区域fundamental parallelepiped。
- 张成空间: 中基向量的所有线性组合(linear combinations)所形成的集合,就叫做这组基向量所张成的空间(SPAN),
- 基础区域:在不包含其他格点的前提下,格基所能张成的区域。【这个概念很重要!!】
如Figure 2阴影部分所示,就是fundamental parallelepiped的示例。假如把维度空间内所有的格点都做一个 , 就能平铺(tiling)掉整个维度空间(span)。一定要注意:格 不能表示整个n维空间, 才能表示整个n维空间。区别就在于span的系数是实数,而格基的系数只能是整数,所以格只能表示一群离散的格点。
正如Figure 2(c)所示它就不是一个格基,那么第一个问题:给定n个m维向量,如何判断它是否是m维空间的一个格基呢?
定理1:格基所生成的基础平行四边形不应该包含除了初始格点(也就是 0 格点)以外的任何格点。
所有的Proof都省略,想了解的去看讲义。
第二个问题是:如何判断两个给定格基是否是等价的?
这里需要引入一个工具幺模矩阵Unimodular matrix:如果一个矩阵的行列式等于正负一,那么就称其为幺模矩阵。比如下面这个矩阵就是一个幺模矩阵:
定理2:幺模矩阵的逆也是幺模矩阵。
定理3:两个格基 是等价的,当且仅当存在某个幺模矩阵 使得 成立。
推论1:一个n维整数空间的格基 必然是一个幺模矩阵。
对于第二个问题还有一个判断方法,需要引入格基的行列式(Determinant)概念。如果格基是一个方阵(即满秩格),格基的行列式直接是方针的行列式;如果格基不是方阵,那么需要使用volumn代替行列式的概念,具体定义为: 。 那么如果两个格基等价,有:
(这里大家可以复习一下多矩阵的行列式运算法则)
格的行列式大小与格子密度成反比,行列式越小,格子越多。
不难看出,虽然格可以刻画 n 维空间离散点集,但是格的行列式,指的是上面提到的「基础区域」的容量volumn。因此,当我们以后提到格的容量时,无特别说明,都是指基础区域的容量。
2. Gram-Schmidt Orthogonalization
在学习线性代数时,施密特正交化是一个非常基础且重要的处理工具。
它的作用是:把一组线性无关向量转化成一组正交的向量。这里推荐知乎上一篇图文并茂的文章。
当我们描述一个点时,我们通常喜欢“直角坐标系”来求坐标,高维空间也是一样。所以我们需要把格基这种「一般坐标系」正交化成「直角坐标系」,便于我们描述空间上某一点。这就是施密特正交化的重要之处。
二维平面的施密特正交化
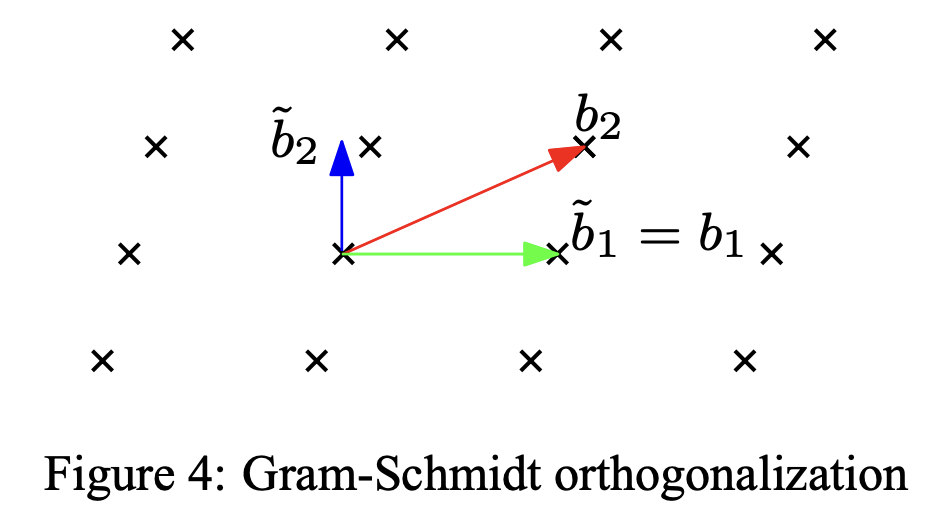
如上图, 是一组线性无关向量,它可以作为二维平面的一个格基。以一个基向量为基准,不妨设 ,利用投影公式可以求另一个向量 在这个向量的投影,再作差得到与基准向量的正交向量: . 同理可知三维平面的格基的施密特正交化步骤:首先选取一个基向量作为基准,利用投影公式求出另一个向量在这个向量的投影,作差得到两条相互正交的向量;对于第三条向量,分别对之前两条正交向量求投影向量,然后用分别减去这两个投影向量,即可得到三条正交向量。
一般形式的施密特正交化
对于n维欧氏空间,设一组基为 ,定义其施密特正交化之后的基向量为 。其中:
上述 记号表示两个向量之间的点乘。
sage中内置了施密特正交化的函数: 对于矩阵 A,直接调用
A.gram_schmidt()
施密特正交化之后的基向量有如下特点:
- 基向量之间两两正交,即其点乘结果为0.
- 原格基与正交后的格基的span是同一张成空间.
- 正交后的格基无需是原格基所形成的格的等价基,甚至,它们一般不在一个格内,见Figure 4.
施密特正交化在维度空间有一个非常有用的用途:计算「容量」volumn。
在二维空间,容量就是面积,在三维空间,容量是体积,在更高维的空间,有更高级的概念。当格满秩时,格基所张成的「基础区域」的容量就可以直接对正交后的格基求行列式即可得到。
3. Successive minima
译为逐次最小长度,或者连续极小。【但是好像叫做最短向量长度更切合】
当我们刻画一个格时,一个基础属性是格的最短非零向量的长度。(格空间中总是存在一个零向量,它的范数norm为0)
范数:是一个定义在向量空间上的函数,它将向量映射到非负实数。直观地说,范数可以理解为“长度”的概念,类似于欧几里得空间中的距离。范数可以用来衡量向量的大小或“长度”,并且在许多数学和应用领域中都有重要的应用。一个向量的范数计作 .
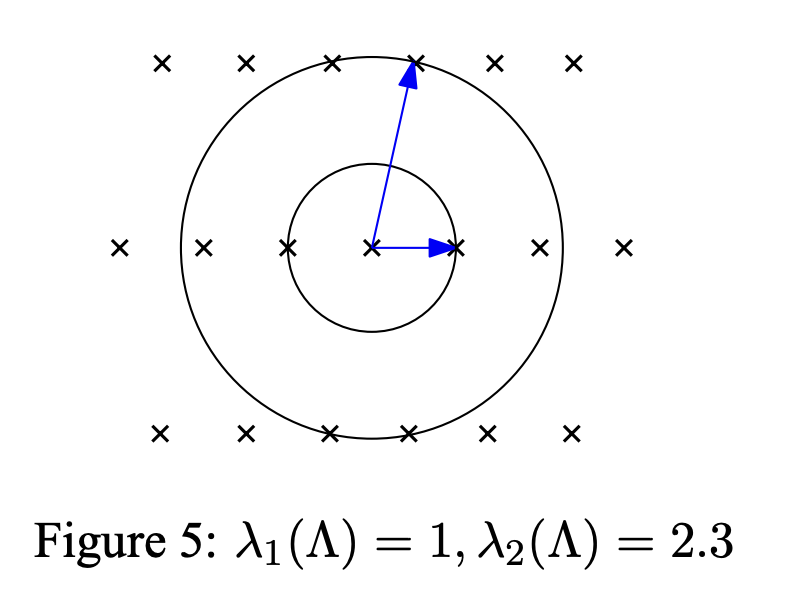
Successive minima这个参数一般计作 . 它主要刻画了格的稀疏程度。
它的另一种定义是:最短向量长度 r 是满足半径为 r 的「n维球」的一维张成空间(一条线)所包含的格点中所能形成的最短向量的长度。
于是我们可以推广到 the i-th successive minima 概念:
其中 表示以0格点为圆心,格点的范数小于等于 r 所构成的n维封闭球。r 就是满足这个球里的点形成的基向量最短的最短半径。
表示格中第 i 短的线性无关向量。
下面开始解释:
- n维球:这里强调n维,我们都知道球ball是一个三维概念,但是在不同维度空间,“球”坍塌或者扩张为其他表现形式,比如一维空间,球是一条线段,一条向量就在一个一维空间里。
- 下图中,假设两个格点的水平距离为1,那么 , 但是 ,因为等于2的向量与 对应的向量是线性相关的。
下面给出如何求 Successive minima 的有效下界:
定理 4: 令 是秩为 n 的格基,令 是其施密特正交化的基,那么:
推论 2:假设 是一个lattice,存在 ,对于任意两个非等格点 ,满足 .
【简单理解就是,在格中,两个不同的格点构成的向量的范数一定大于0,是非零向量】
断言 1:如果一个格 最短向量长度存在,那么对于 格中一定存在某个 满足
这里需要弄清楚一个事实:successive minima对应的最短向量不一定是格基。【如figure 4】
successive minima的上界
定理 4 给出了如何利用施密特正交化求得最短向量的下界,那么如何求它的上界呢?Minkowski给出了一个答案。
为了简单,我们考虑满秩格,非满秩格可以很简单的延伸。首先介绍一下 Blichfeld 定理:
定理 5 (Blichfeld):任何满秩格 和集合 ( ), 存在集合中两个不同的点,使得这两个点构成的向量属于格空间。
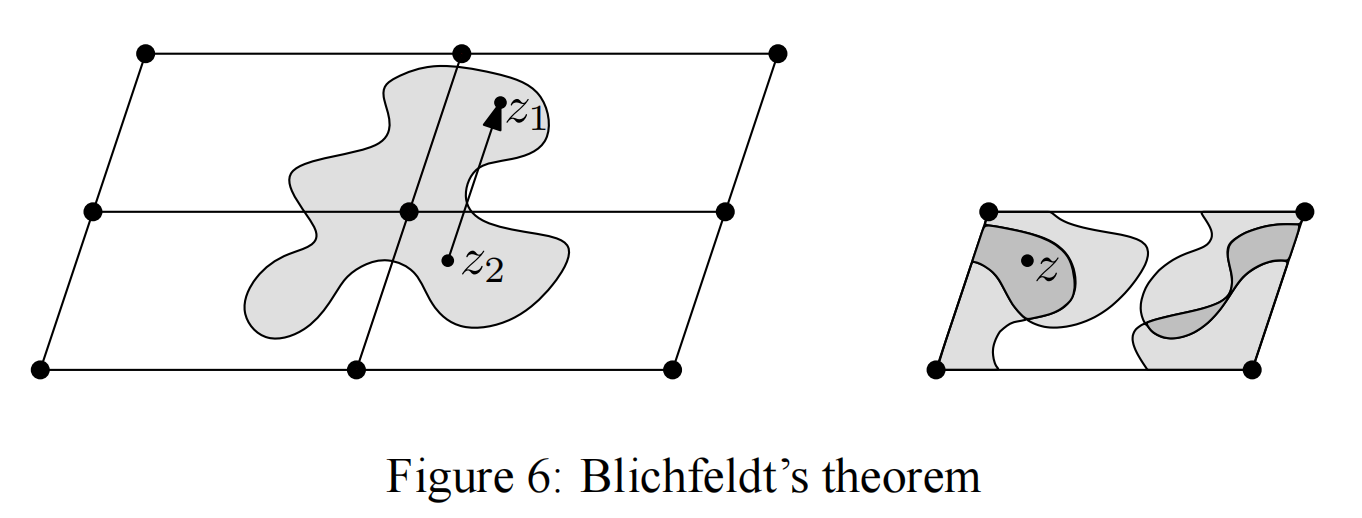
如图Figure 6,正如前面所说的,格的行列式表示的基础区域的容量。
定理 6(Minkowski’s Convex Body Theorem):若 是一个秩为 n 的格,那么对于任意一个中心对称的凸体 ,如果 ,那么 中存在一个非零格点。
断言 2:半径为 r 的 n 维球的体积volumn为: .
推论 3(Minkowski’s First Theorem) : 对于任意秩为 n 的满秩格 , 有:
Minkowski’s First Theorem 给出的上界不一定很紧致tight。
还有 Minkowski’s Second Theorem:
综上所述,施密特正交化给出了格的最短向量的下界,Minkowski’s First Theorem给出了满秩格的最短向量的上界。
4. Computational problems
经过上述介绍,我们可以看到,对于格的最短向量(非0)的只有一个大概的上下界,而我们目前没有有效算法找出最短向量。这就引出了我们在开头所述的底层数学难题,关于格的数学难题大概有两类:SVP和CVP。与密码学经典的数学难题一样(DLP,CDH,DDH…),关于格的数学难题也有很多变种,下面分别介绍一下。
Shortest Vector Problem(SVP)
SVP难题的变种也是根据难度划分为:是否真的需要找到最短向量?只需要找到最短向量的长度?或者甚至只要确定最短向量比某个给定的值小即可?具体是:
- Search SVP:给定格基,找出最短向量。
- Optimization SVP:给定格基,找出最短向量长度(Successive Minima)即可。
- Decisional SVP:给定格基和一个有理数,判断格的最短向量长度是否比它小即可。
注意:以上难题中,均限制格基向量为整数向量,这要做的目的是为了输入可以用有限比特来表示,因此我们可以将SVP当做一个标准计算问题。我们也可以允许格基由有理向量组成。这将导致一个本质上等效的定义,因为通过缩放,可以使所有有理坐标为整数。
这三个变种,Search SVP、Optimization SVP和Decisional SVP的难度依次下降,但是反之亦然。因此,这三个难题是等价的。
在 Regev 课程中,考虑的是 SVP 的近似变体,近似因子 :
- Search :给定格基,找出近似最短向量。
- Optimization :给定格基,找出最短向量长度的近似范围即可。
- Promise :给定格基和一个有理数 r ,如果是 YES 实例,判断格的最短向量长度是否小于等于 r 即可;如果是 NO 实例,判断格的最短向量长度是否大于 即可
最后一种也叫做 ,这种情况下每个实例都有特定的输入集合,如果输入不在这些集合中,将会导致未定义行为。
同样的,promise变体并不比optimization变体更困难,optimization变体不比Search变体更困难。反之,optimization变体不比promise变体更困难,但是Seach变体是否比optimization变体更困难尚且是一个开放问题。
Closest Vector Problem(CVP)
顾名思义,这个数学难题是为找到给定格点的最近格点。与 SVP 一样,对 CVP 也定义了三种变体:
- Search :给定格基 和 向量 ,找到另一个向量 满足 .
- Optimization :给定格基 和 向量 ,找到距离 d 满足 .
- Promise :给出一个CVP实例三元组 ,如果是 YSE 实例, ;如果是 NO 实例, .
以上两种都是计算难题。关于格还有一些易于计算的问题,比如:
- 成员关系:给定格基和向量,判定向量是否属于格。这个问题可以使用高斯消元法(Gaussian elimination)高效解决。
- 等价关系:给定两个格基,判定二者是否等价。这个问题可以按列判断包含关系,然后两者交换再检查包含关系。如果都成立,则说明二者等价。