- 作者:Maksym Petkus
- 翻译 & 注解:even@安比实验室([email protected])
- 校对:valuka@安比实验室
- 本系列文章已获作者中文翻译授权
- 翻译原链接
- Computation
- Single Operation
- Enforcing Operation
- Proof of Operation
- Variable Polynomials
- Reference :
Computation
Let us consider a simple program in pseudocode:
Algorithm 1: Operation depends on an input
—————————————————————————————————————————————————————————
function calc(w, a, b)
if w then
return a × b
else
return a + b
end if
end function
Therefore we need to find a way to convert a program into the polynomial form , like this
Executing and evaluating will yield the same result: 8. and would both be resolved to 6. We can express any kind of finite program in such a way.
猜想一下,是否只要是能够用多项式表示的程序都可以做证明?
Single Operation
Any computation at it is core consists of elemental operations of the form:
If we can represent operand values as polynomials (and we indeed can as outlined) then through the arithmetic properties, we will be able to get the result of an operation imposed by an operand. (如果我们可以将操作数的值表示为多项式(我们也确实可以这么做),那么利用算术属性,我们就能够得到操作数的计算结果了。)
@Even : 回忆一下,在本系列的第一篇——多项式的性质与证明中,我们曾经说过“任何多项式在任意点的计算结果都可以看做是其唯一身份的表示。”
反过来当我们知道某个多项式的时候,是不是也就意味着我们知道多项式上某个点的取值。这就是借助多项式来完成证明的依据。
Enforcing Operation
如果一个 prover 声称有某 2 个数字的乘积,verifier 要怎样去验证呢?
Recap computation form, 我们也可以将其表示为一个运算多项式 :
在计算过程中, 如果操作数(operands) 和 结果(output) 都能用多项式的形式正确地表示出来,那么 就应该成立
也就表明, 当取值为 时, 多项式 成立,
即该多项式一定有一个根 , 因此,这个多项式里面一定包含因式(cofactor) , 这就是我们要证明的目标多项式(target polynomial) ,即
For example, let us consider operation:
可以用一个简单的多项式表示它: 取 ,即
运算多项式就变成了 :
因而如果 用多项式 来代替 ,因其依然可被 整除,所以 就认可其是有效的
相反,如果 prover 尝试用 , 即 来代替输出值去欺骗 verifier ,即 ,那么运算多项式就变成了 , 这个多项式并没有 的解,因而 不能被 整除:

在前面的协议中,我们要证明的多项式是 ,这里我们把 替换成 , 这仍然是被 承认有效的。这里目标多项式 的根就是对应能够计算出数学表达式的值的
上面例子里面取 作为运算编码的位置, 1 可以换成任何别的值,比如说 .. 在 [GGPR] 与 [PHGR] 论文中,这个取值是一个随机值,被称为 “root”
Proof of Operation
前面多项式的 SNARK一章,我们已经能够证明多项式 的知识了,只不过现在要计算的是三个多项式 的知识。我们可以定义 ,但这里存在两个争议点。
- ① 在我们的协议中, 证明阶段是不能做加密值乘法计算的 (即 ),因为 Pairing 只能用一次(不能复用, 会有安全风险?) —— Pairing 要用在校验多项式的约束上
- ② 这里给证明者留下了一个可以修改多项式结构(修改知识) 但依然保留有效因式 的机会,for example or or even —— 只需要 有一个根 就可以骗过 , 这样是不行的 !
所以 必须要 分别提供 多项式 值的证明,即协议必须修改要证明的多项式的知识( knowledge of polynomial must be adjusted.)
In essence(本质上), 在加密空间中要验证的是 .
即使 可以用 Pairing 来执行乘法(multiplication),但在 Pairing 中做减法 ( ) 是非常昂贵的计算(would require to find inverse of ),所以咱们把 移到右边:
在加密空间中, 的验证就可以转换成:
Red Part: recall that the result of cryptographic
pairingssupports encrypted addition through multiplication, see section on pairings.
保持 setup 阶段不变,协议更新为:

这个协议就能够证明两个值相乘的计算结果是正确的了。
你可能注意到了在这个新的协议中我们放弃了 - 零知识 部分。这么做是为了简化协议, 后面的章节我们会再变回零知识 ~
even@安比实验室:上面例子里面取 这个特殊值作为运算编码的位置。当然这里的 1 可以换成任何别的值,比如说换成 等等。在[GGPR] 与 [PHGR] 论文中,这个取值是一个随机值,被称为 “root”
名词定义
operand : 符号左边叫 left operand , right operand
- 是具体的操作数, 比如 里的 a & b ; 里的 2 & 3
oprand polynomials : l(x) and r(x).
- left operand polynomial (green) 几个约束等式的操作数左边竖列, 构成的 poly 叫 left operand polynomial
- right operand polynomial (blue) ….
output polynomials : 等式右边的所有 Output 操作数 竖列 构成的 poly 叫 output polynomials
Multiple Operations
We can prove a single operation, but how do we scale(拓展) to prove (which is our ultimate goal)? Let us try to add just one another operation. Consider the need to compute the product: :
来看一个有三个乘法运算的例子 2 × 1 × 3 × 2,它按照下面的步骤执行:
我们要把它们表示为多项式,对于 , 相应的要 。 即通过点 , 同样的: ,
we use Polynomial Interpolation to represent these.
Interpolation Result :
Multi-Operation Polynomials
Now we have operand polynomials , let us see step-by-step how the correctness of each operation is verified.
Recall that a verifier is looking for equality .
本例中,计算是在点 处被表示出来的,所以 target poly 在这些点处必须 evaluation 为 ,换句话说, 的根 root 必须是 1,2 和 3,它的基本形式就是:
在实际过程中, 一般是放到单位根 root of unity —— 里的
Firstly, are multiplied which results in:
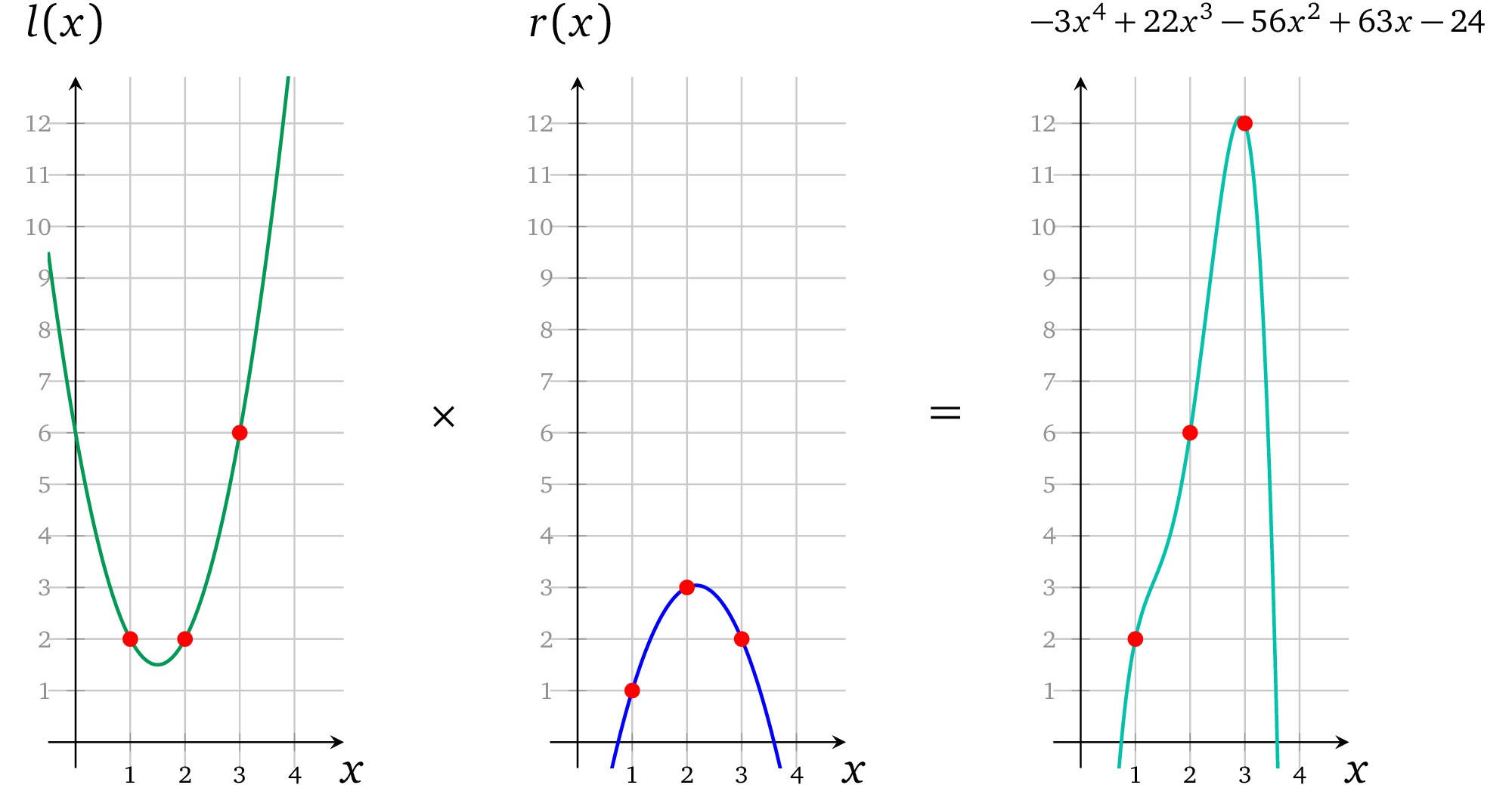
Secondly, the is subtracted from the result of which is :

已经可以看出每一个 operands multiplication 都对应了正确的结果。最后一步 要算出一个有效因式:
通过长除法(long division) 可以算出: :
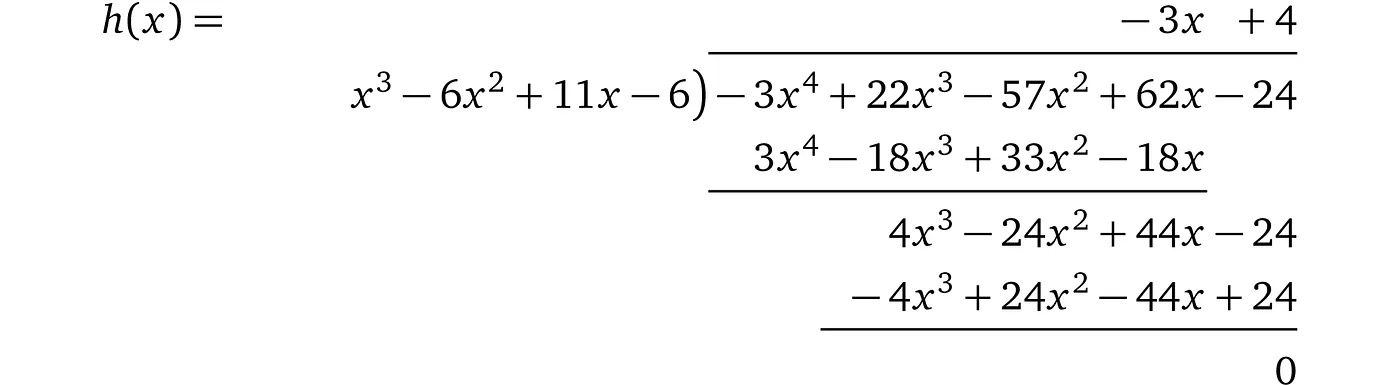 自己代入 , 可以自己计算 :
> PS: 这里为了简化过程, 省略了完整协议中的 `δ-zero-knowledge` 和 `α-shift`
自己代入 , 可以自己计算 :
> PS: 这里为了简化过程, 省略了完整协议中的 `δ-zero-knowledge` 和 `α-shift`
现在显然 ,这就是我们要证明的内容。
这里只用了一组多项式 就将所有计算的约束关系表示出来了,有几步计算, 也就对应着目标多项式 要有几个根 (这里我这么理解: 计算的步数多了, 那么 的根也就多了, 比如可能是 , 因为约束等式的行数多了, 也就需要同步约束这些等式符合所有的计算完整性验证 )
当前的协议似乎存在一些缺陷,多项式只能证明 拥有一组多项式 ,在 的几个根的取值处 ,但无法证明这组多项式符合我们要证明的数学表达式: 1)多个计算关系之间也是分开表示的,这些算式之间的关系也同样无法进行约束 2)由于 生成的证明中只有计算结果,左操作数,右操作数,输出在计算中混用也不会被发现 3)由于左操作数,右操作数,输出是分开表示的,他们互相之间的关系无法进行约束
Variable Polynomials
现在我们可以一次证明多个运算(如上百万个甚至更多)了,但是前文结尾提到了几个关键缺点(critical downside)
如果证明中执行的“程序“在不同运算中使用了相同的变量作为操作数或输出,例如:
然而,因为我们的协议中是允许 为多项式设置任何系数的,所以他可以不受限制得为不同计算中的 设置不同的值,如:
 This freedom breaks **consistency** and allows to prove the execution of some other program which is not what verifier is interested in. (**这种自由打破了一致性**, 允许 去证明一些无关的程序执行)
This freedom breaks **consistency** and allows to prove the execution of some other program which is not what verifier is interested in. (**这种自由打破了一致性**, 允许 去证明一些无关的程序执行)
Therefore we must ensure that any variable can only have a single value across every operation it is used in. (因而我们必须要确保每一个变量在所有运算中出现的地方都只有一个取值。)
注意:文中的
variable与常规的计算机科学中variable的定义不同,这里的变量是不可改变的(immutable), 而且每次执行都只赋值一次(only assigned once per execution) (即示例伪代码中的那些不会被修改的变量)zkSNARK 论文中,这个「变量」其实有一个对应的名词叫做
assignment,是算术电路的「赋值」,对应的是问题结构或者说算术电路的结构。而所有的 assignments 是一个算术电路可满足性问题的解,包含了算术电路的输入值以及电路运算过程中输出的中间结果值 (没看懂这里)
Single-Variable Operand Polynomial
那么, How to ensure 每一个变量在所有运算中出现的地方都只有一个取值? 究其原因, 可以设置不同值是因为他可以任意控制 的系数 a malicious 可以分别为第一第二行的 分配不同的值, 比如分别分配 和 :
- assign for in raw ① , 那么此处 的系数为 , 即函数通过点
- assign for in raw ②, 那么此处 的系数为 , 即函数通过点
此时就出现了不一致问题 —— 那么如果对于同一个变量 , 这些系数是固定的,就可以解决问题了
如下是 2 个包含相等值的多项式 : 它们分别都表示了有两个相等值对应的运算(即在 和 处),第一个多项式的取值为 1,第二个多项式的取值为 2:

注意: 这 2 个多项式的相应的系数是成比例的 —— 第 2 个多项式的系数是第 1 个的 2 倍
那么由于多项式的算术性质,如果我们想要同时地改变多项式中所有的值 , 我们就需要改变它的比例,如果我们用一个数字 乘以多项式,那么多项式值就会等比例变换为 倍
Consequently, if a verifier needs to enforce the prover to set the same value in all operations, then it should only be possible to modify the proportion and not the individual coefficients.
(因此,如果 需要在所有计算中强制 设置相同的值,他就要限制 只能改动多项式的比例, 而不是恣意篡改某处操作的单个系数)
怎么保持系数比例不变呢?对于这个问题我们可以先思考一下在 左运算多项式 (left operand polynomial) 中我们提供的 Proof 是什么 —— 是 在一些秘密值 处的加密值:
上文中, 我们已经知道怎样通过 α-shift 去限制 只能使用 (或 ) 提供的 的幂做计算,来使得单个运算能够满足同态乘法 (such that homomorphic multiplication is the single operation available.)
和限制单个求幂值相似, 可以一次限制完整的多项式 。而不只是提供单独的加密及其 α-shift :
协议的过程是:
Setup :
- 使用多项式对应的系数构造相应的 operand polynomial
- 创造随机 secret
- 使用加密的 和它的 ”α-shifted“ : 来设置 proving key
- 设置 verification key:
Proving :
- 注意这个语境下, 对应的操作数只有 一个 (Recall ① ② 两个等式) , 所以若 赋值为 , 则第① 第② 个等式里, 都要保持 的赋值为
- 对 的操作数 的赋值为
- 将其乘以操作数多项式:
- 乘以
α-shifted后的 operand polynomial :
- 提供 operand polynomial multiplication Proof :
这里的
multiplication就是指通过 来限制 对 operand polynomial 只能提供相同的 assignment
Verification
- Parse the Proof as
- Pairing 验证比例

前面反复提到, needs to respond with the same α-shift , and because he cannot recover α from the proving key , the only way to maintain the shift is to multiply both encryptions by the same value :
同样的道理, 用这种方法可以限制 让其无法修改 的单个系数 (modify individual coefficients of ) , 如果多项式为 , 只可以用一个值 去 multiply 整个多项式一次:
Multiplication by another polynomial is not available since pairings, and α-shifts of individual exponents of s are not provided. Prover cannot add or subtract either since:
This requires the knowledge of unencrypted , 这里也同样需要未加密的 的知识(才能运算)
详细解释一下 上式 :
- 考虑 ,如果 能够任意修改多项式的系数,他可能会想要构造一个新的多项式 来欺骗
- 但是, 无法实现这样的操作,因为他不知道确切的 的值 , 最后的等式是为了展示这一限制:
- 左侧: 需要满足 α-shift, 通过这种方式修改 的各个系数
- 右侧: 提供了 , 但没有提供 , 所以 无从得知 , 所以 只能提供可怜的 , 而这是无法通过 Pairing 验证的
现在有了这个协议,不过怎么去构造 operand polynomial 呢?由于任何整数都可以通过乘以 1 得到它本身,所以多项式中对应的每个计算结果都应该为 1 ,即:
 > (这里的表述不清晰, 很多人没看懂, 我个人觉得类似拉格朗日基, 后面多变量会讲到: 用到了就设置为 1, 用不到就设为 0)
> (这里的表述不清晰, 很多人没看懂, 我个人觉得类似拉格朗日基, 后面多变量会讲到: 用到了就设置为 1, 用不到就设为 0)
然后再让 prover 在其上”分配“一个值 a :

Remark 4.1 : 可以在操作数多项式上分配一个 ,而 不能检测到 , 下面具体描述了 对多项式进行特定加(或减)操作的能力,而这种操作不会影响 配对验证 , 因而可以修改多项式使其超出 的预期 或 prove a different statement,后面的章节我们将会解决掉这个问题 :
identically equal: 恒等
由于 verification key 中包含了加密了的 : , 所以 可以用多项式加(或者减)任意一个值 而不会破坏 Pairing 的成立. 后面我们会解决掉这个 bug
Summary/Recap
这一小节是解决这样一个问题,算术电路中一个 input wire 或者 output wire可能同时会作为多个门的输入 wire,如何确保约束这些公用 wire 的问题。
由于要证明的数学表达式是公开的,那么各个算式之间的约束关系也就是公开的,那么我们就可以把构造多项式的工作交给 环节,这样 只要填上对应的数值就可以了。
上文这个方法就限制了在同一个操作数多项式上,不同的计算式中使用的同一个值的约束关系;同样若一个操作数多项式中用到了多个值,也可以将这些值全都加起来,如下文所述。
Multi-Variable Operand Polynomial
如上文, 因为只有当所有的左操作数使用同一个变量 的时候我们才可以设置一个值。但是如果左操作数中再多一个值 要怎么做呢 ?

Therefore we can separate the operand polynomial into 2 operand variable polynomials :
变量 和 可以被分别 赋值 & 约束,然后加在一起 , 来表示所有的左操作数变量。
如果 多变量多项式 在一个对应运算中被用做操作数,那么这一项就置为 1,否则就置为 0 , 0 跟任何值相乘结果都是零,当把他们相加在一起的时候也就可以忽略掉这一项 (类似 Lagrange Basis 的作用) 在我们的例子中, 这些变量多项式必须满足以下计算:

于是我们就可以将每个变量分开 assigned value ,然后把他们加在一起来计算出操作数多项式,例如当 和 时 , 得到 :

上图中的 代表: 用 3 实例化的变量 ( variable instantiated with value 3 )
从现在起 , 我们用大写的 来表示这个复杂的操作符多项式,即
仅当每一个 operand variable polynomial 是由 约束的 (restricted by the ),结果才有效
以 left operand 部分而言, 协议部分更改为:
Setup:
- 构造 - 使得它能够在对应的
"operation x"处为 1,其他地方为 0 - 选择随机数
- 计算并加密 未赋值的变量多项式 (unassigned variable poly):
- 计算 shifts of these polys :
- set proving key :
- set verification key:
Proving :
- assign values to the variable polys : {\left(g^{l_a(s)}\right)}^\textcolor{green}{a}, \ \ {\left(g^{l_d(s)}\right)}^\textcolor{green}{d}
- assign same values to the
α-shiftedpoly : - add all assigned variable polys to form a operand poly :
- add shifted assigned variable polys to form a shifted operand poly :
- Proving proof of valid assignment of left operand :
Verification :
- Parse Proof i.e.
- 验证提供的多项式是否是 最初提供的多个 未赋值的变量多项式 (unassigned variable poly) 的和:
Note: and represent all variable polynomials at once and since is used only in evaluation of variable polynomials, the prover has no option but to use provided evaluations and assign same coefficients to original and shifted variable polynomials. ( 注意:这里用 和 同时代表了所有的变量多项式, 并且由于 只用在计算变量多项式中,所以 没有别的选择只能在 提供的原始加密值和变换后的加密值上赋予相同的系数做计算 )
As a consequence(因此) the prover :
- is not able to modify provided variable polynomials by changing their coefficients, except “assigning” values (除了“分配”值外,不能再修改它们的系数进而来修改 变量多项式 ), because prover is presented only with encrypted evaluations of these polynomials, and because necessary encrypted powers of s are unavailable separately with their α-shifts (因为 Prover 仅提供这些多项式的加密评估,也因为 s 必要次幂的加密值不能与它们的 α 变换值一起使用 )
- is not able to add another polynomial to the provided ones because the α-ratio will be broken (不能通过另一个多项式相加去提供一个结果因为这样 α-比例关系将会被破坏掉)
- is not able to modify operand polynomials through multiplication by some other polynomial , which could disproportionately modify the values because encrypted multiplication is not possible in pre-pairings space (不能通过与其他的一些多项式 相乘来修改操作数多项式,这样可能会使得修改后的值不成比例因为在预配对空间中无法进行加密乘法)
尽管 prover 被限制了多项式的使用,他还有拥有一些可允许范围内的自由度:
- 当 prover 决定不加入一些变量多项式 来构造操作符多项式 时依然是可以接受的,因为这和为它分配值为 0 是一样的:
- 如果 添加同一个
变量多项式很多次也是可以接受的 , 因为这和一次分配多个值的和是一样的:
Summary/Recap
总结一下本文证明协议的大致思路为:
- 将要证明的程序转换为数学语言表达的形式(即加减乘除的计算)
- 用多项式在某处的取值来进行计算以此表示数学计算,进而进行证明
- 用多项式在多处的取值来进行计算表示多个数学运算,进而加以证明
- 对证明的“程序”在不同计算中使用的相同的变量进行约束
当前的协议约束只解决了部分问题,还有诸多可以改进的地方,在下一节我们将对这些改进项展开讨论并给证明协议进行优化。
Reference :
- https://secbit.io/blog/2020/01/08/learn-zk-snark-from-zero-part-three/
- https://medium.com/@imolfar/why-and-how-zk-snark-works-4-general-purpose-computation-dcdc8081ee42
- https://medium.com/@imolfar/why-and-how-zk-snark-works-5-variable-polynomials-3b4e06859e30