理解 PLONK（四）：算术约束与拷贝约束

回顾置换证明

上一节，我们讨论了如何让 Prover 证明两个长度为 $N$ 的向量 $a$ 与 $b$ 满足一个实现约定（公开）的置换关系 $σ (\cdot)$ ，即

$a_{i} = b_{σ (i)}$

基本思路是向 Verifier 要一个随机数 $β$ ，把两个「原始向量」和他们的「位置向量」进行合体，产生出两个新的向量，记为 $a^{'}$ 与 $b^{'}$

$a_{i}^{'} = a_{i} + β \cdot i, b_{i}^{'} = b_{i} + β \cdot σ (i)$

第二步是再向 Verifier 要一个随机数 $γ$ ，通过连乘的方法来编码 $a^{'}$ 和 $b^{'}$ 的 Multiset，记为 $A$ 和 $B$ ：

$A = \prod (a_{i}^{'} + γ), B = \prod (b_{i}^{'} + γ)$

第三步是让 Prover 证明 $A / B = 1$ ，即

$i \prod \frac{( a _{i}^{'} + γ )}{( b _{i}^{'} + γ )} = 1$

证明这个连乘，需要引入一个辅助向量 $z$ ，记录每次乘法运算的中间结果：

$z_{0} = 1, z_{i + 1} = z_{i} \cdot \frac{( a _{i}^{'} + γ )}{( b _{i}^{'} + γ )}$

由于 $z_{N} = \prod \frac{a _{i}^{'} + γ}{b _{i}^{'} + γ} = 1$ ，而且 $ω^{N} = 1$ ，因此我们可以用 $z (X)$ 来编码 $z$ ，从而把置换证明转换成关于 $z (X), a (X)$ 的关系证明。

最后 Verifier 发送挑战数 $ζ$ ，得到 $z (ζ), z (ω \cdot ζ), a (ζ), b (ζ)$ 然后检查它们之间的关系。

向量的拷贝约束

所谓拷贝约束 Copy Constraints，是说在一个向量中，我们希望能证明多个不同位置上的向量元素相等。我们先从一个简单例子开始：

$a = (a_{0}, a_{1}, a_{2}, a_{3})$

假设为了让 Prover 证明 $a_{0} = a_{2}$ ，我们可以把 $a_{0}$ 与 $a_{2}$ 对调位置，这样形成一个「置换关系」，如果我们用 $(0, 1, 2, 3)$ 记录被置换向量的元素位置，那么我们把置换后的位置向量记为 $σ$ ，而 $a_{σ}$ 为表示按照 $σ$ 置换后的向量

$σ = (2, 1, 0, 3), a_{σ} = (a_{2}, a_{1}, a_{0}, a_{3})$

显然，只要 Prover 可以证明置换前后的两个向量相等， $a = a_{σ}$ ，那么我们就可以得出结论： $a_{0} = a_{2}$ 。

这个方法可以推广到证明一个向量中有多个元素相等。比如要证明 $a$ 中的前三个元素都相等，我们只需要构造一个置换，即针对这三个元素的循环右移：

$σ = (2, 0, 1, 3), a_{σ} = (a_{2}, a_{0}, a_{1}, a_{3})$

那么根据 $a = a_{σ}$ 容易得出 $a_{0} = a_{1} = a_{2}$ 。

多个向量间的拷贝约束

对于 Plonk 协议，拷贝约束需要横跨 $W$ 表格的所有列，而协议要求 Prover 要针对每一列向量进行多项式编码。我们需要对置换证明进行扩展，从而支持横跨多个向量的元素等价。

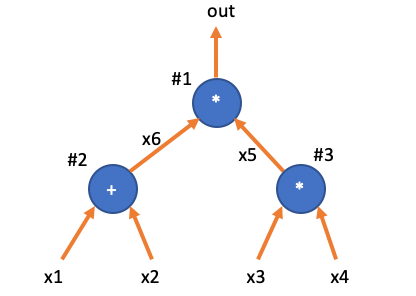
回忆比如针对上面电路的 $W$ 表格：

$i 0123 w_{a} 0 x_{6} x_{1} x_{3} w_{b} 0 x_{5} x_{2} x_{4} w_{c} o u t o u t x_{6} x_{5}$

看上面的表格，我们要求 $w_{a, 1} = w_{c, 2}$ ， $w_{b, 1} = w_{c, 3}$ 且 $w_{c, 0} = w_{c, 1}$ 。

支持跨向量置换的直接方案是引入多个对应的置换向量，比如上表的三列向量用三个置换向量统一进行位置编码：

$i 0123 i d_{a, i} 0123 i d_{b, i} 4567 i d_{c, i} 891011$

置换后的向量为 $σ_{a}, σ_{b}, σ_{c}$ ：

$i 0123 σ_{a, i} 01023 σ_{b, i} 41167 σ_{c, i} 9815$

Prover 用一个随机数 $β$ （Verifier 提供）来合并 $(w_{a}, i d_{a})$ ， $(w_{b}, i d_{b})$ ， $(w_{c}, i d_{c})$ ，还有置换后的向量： $(w_{a}^{'}, σ_{a})$ ， $(w_{b}^{'}, σ_{b})$ ， $(w_{c}^{'}, σ_{c})$ 。然后再通过一个随机数 $γ$ （Verifier 提供）和连乘来得到 $W$ 和 $W^{'}$ 的 Multisets， ${f_{i}}$ 与 ${g_{i}}$

$f_{i} g_{i} = (w_{a, i} + β \cdot i d_{a, i} + γ) (w_{b, i} + β \cdot i d_{b, i} + γ) (w_{c, i} + β \cdot i d_{c, i} + γ) = (w_{a, i}^{'} + β \cdot σ_{a, i} + γ) (w_{b, i}^{'} + β \cdot σ_{b, i} + γ) (w_{c, i}^{'} + β \cdot σ_{c, i} + γ)$

又因为拷贝约束要求置换后的向量与原始向量相等，因此 $w_{a} = w_{a}^{'}$ ， $w_{b} = w_{b}^{'}$ ， $w_{c} = w_{c}^{'}$ 。

如果我们用多项式对 $w_{a}, w_{b}, w_{c}, i d_{a}, i d_{b}, i d_{c}, σ_{a}, σ_{b}, σ_{c}$ 编码，得到 $w_{a} (X), w_{b} (X), w_{c} (X), i d_{a} (X), i d_{b} (X), i d_{c} (X), σ_{a} (X), σ_{b} (X), σ_{c} (X)$ ，于是 $f (X)$ ， $g (X)$ 满足下面的约束关系：

$f (X) g (X) = (w_{a} (X) + β \cdot S_{i d_{a}} (X) + γ) (w_{b} (X) + β \cdot S_{i d_{b}} (X) + γ) (w_{c} (X) + β \cdot S_{i d_{c}} (X) + γ) = (w_{a} (X) + β \cdot S_{σ_{a}} (X) + γ) (w_{b} (X) + β \cdot S_{σ_{b}} (X) + γ) (w_{c} (X) + β \cdot S_{σ_{c}} (X) + γ)$

如果两个 Multiset 相等 {f_i\}={g_i}，那么下面的等式成立：

$X \in H \prod f (X) = X \in H \prod g (X)$

上面的等式稍加变形，可得

$X \in H \prod \frac{f ( X )}{g ( X )} = 1$

我们进一步构造一个辅助的累加器向量 $z$ ，表示连乘计算的一系列中间过程

$z_{0} = 1, z_{i + 1} = z_{i} \cdot \frac{f _{i}}{g _{i}}$

其中 $z_{0}$ 的初始值为 $1$ ，Prover 按照下表计算出 $z$ ：

$i 0123 ⋮ N - 1 N H_{i} ω^{0} = 1 ω^{1} ω^{2} ω^{3} ω^{N - 1} ω^{N} = 1 z_{i} 1 1 \cdot \frac{f _{0}}{g _{0}} \frac{f _{0}}{g _{0}} \cdot \frac{f _{1}}{g _{1}} \frac{f _{0} f _{1}}{g _{0} g _{1}} \cdot \frac{f _{2}}{g _{2}} ⋮ \frac{f _{0} f _{1} \dots f _{N - 3}}{g _{0} g _{1} \dots g _{N - 3}} \cdot \frac{f _{N - 2}}{g _{N - 2}} \frac{f _{0} f _{1} \dots f _{N - 1}}{g _{0} g _{1} \dots g _{N - 1}} = 1$

如果 $f$ 能与 $g$ 连乘等价的话，那么最后一行 $z_{N}$ 正好等于 $1$ ，即

$z_{N} = z_{0} = 1$

而又因为 $ω^{N} = 1$ 。这恰好使我们可以把 $(z_{0}, z_{1}, z_{2}, \dots, z_{N - 1})$ 完整地编码在乘法子群 $H$ 上。因此如果它满足下面两个多项式约束，我们就能根据数学归纳法得出 $z_{N} = 1$ ，这是我们最终想要的「拷贝约束」：

$z (ω^{0}) = 1$

$z (ω \cdot X) g (X) = z (X) f (X)$

置换关系 $σ$

在构造拷贝约束前，置换关系 $σ$ 需要提前公开共识。表格 $W$ 含有所有算术门的输入输出，但是并没有描述门和门之间是否通过引线相连，而置换关系 $σ$ 实际上正是补充描述了哪些算术门之间的连接关系。

因此，对于一个处于「空白态」的电路，通过 $(Q, σ)$ 两个表格描述，其中 $Q$ 由选择子向量构成，而 $σ$ 则由「置换向量」构成。

下面是 $Q$ 表格

$i 0123 q_{L} 0010 q_{R} 0010 q_{M} 0101 q_{C} 99000 q_{O} 1111$

下面是 $S$ 表格，描述了哪些位置做了置换

$i 0123 σ_{a, i} 01023 σ_{b, i} 4 \underline{11} 67 σ_{c, i} [9] [8] 1 \underline{5}$

处理 Public Inputs

假如在上面给出的小电路中，要证明存在一个 Assignment，使得 out 的输入为一个特定的公开值，比如 $o u t = 99$ 。最简单的办法是使用 $Q$ 表中的 $q_{C}$ 列，并增加一行约束，使得 $q_{L} = q_{R} = q_{M} = 0$ ，因此满足下面等式

$q_{C} (X) - q_{O} (X) w_{c} (X) = 0$

但这个方案的问题是：这些公开值输入输出值被固定成了常数，如果公开值变化，那么 $q_{C} (X)$ 多项式需要重新计算。如果整体上 $W$ 表格的行数比较大，那么这个重新计算过程会带来很多的性能损失。

能否在表格中引入参数，以区分电路中的常数列？并且要求参数的变化并不影响其它电路的部分？这就需要再引入一个新的列，专门存放公开参数，记为 $ϕ$ ，因此，算术约束会变为：

$q_{L} (X) w_{a} (X) + q_{R} (X) w_{b} (X) + q_{M} (X) w_{a} (X) w_{b} (X) - q_{O} (X) w_{c} (X) + q_{C} (X) + ϕ (X) = 0$

我们还可以通过修改拷贝约束的方式引入公开参数。

[!TODO]

位置向量的优化

我们上面在构造三个 $σ$ 向量时，直接采用的自然数 $(0, 1, 2, \dots)$ ，这样在协议开始前，Verifier 需要构造 3 个多项式 $S_{i d_{a}} (X), S_{i d_{b}} (X), S_{i d_{c}} (X)$ ，并且在协议最后一步查询 Oracle，获得三个多项式在挑战点 $X = ζ$ 处的取值 $(S_{i d_{a}} (ζ), S_{i d_{b}} (ζ), S_{i d_{c}} (ζ))$ 。

思考一下， $σ$ 向量只需要用一些互不相等的值来标记置换即可，不一定要采用递增的自然数。如果我们采用 $H = (1, ω, ω^{2}, \dots)$ 的话，那么多项式 $i d_{a} (X)$ 会被大大简化：

$i d_{a} i d_{b} i d_{c} = (1, ω, ω^{2}, ω^{3}) = (k_{1}, k_{1} ω, k_{1} ω^{2}, k_{1} ω^{3}) = (k_{2}, k_{2} ω, k_{2} ω^{2}, k_{2} ω^{3})$

其中 $k_{i}$ 为互相不等的二次非剩余。

$i d_{a} (X) = X, i d_{b} (X) = k_{1} \cdot X, i d_{a} (X) = k_{2} \cdot X$

这样一来，这三个多项式被大大简化，它们在 $X = ζ$ 处的计算轻而易举，可以直接由 Verifier 完成。

这个小优化手段最早由 Vitalik 提出。采用 $k_{1}$ 和 $k_{2}$ 是为了产生 $(1, ω, ω^{2}, ω^{3})$ 的陪集（Coset），并保证 Coset 之间没有任何交集。我们前面提到 $H = (1, ω, ω^{2}, ω^{3})$ 是 $F$ 的乘法子群，如果 $H_{1} = k_{1} H$ 和 $H_{2} = k_{2} H$ 存在交集，那么 $H_{1} = H_{2}$ 。这个论断可以简单证明如下：如果它们存在交集，那么 $k_{1} ω^{i} = k_{2} ω^{j}$ ，于是 $k_{1} = k_{2} \cdot ω^{j - i}$ ，又因为 $ω^{j - i} \in H$ ，那么 $k_{1} \in H_{2}$ ，那么 $\forall i \in [N] . k_{1} \cdot ω^{i} \in H_{2}$ ，那么 $H_{1} \subset H_{2}$ ，同理可得 $H_{2} \subset H_{1}$ ，于是 $H_{1} = H_{2}$ 。

如果 $σ$ 的列数更多，那么我们需要选择多个 $k_{1}, k_{2}, k_{3}, \dots$ 且 $(k_{i} / k_{j})^{N} \neq = 1$ 来产生不相交的 Coset。一种最直接的办法是采用 $k_{1}, k_{2}, k_{3}, \dots = g^{1}, g^{2}, g^{3}, \dots$ ，其中 $g$ 为乘法子群 $T$ 的生成元， $∣ T ∣ * 2^{λ} = p - 1$ 。

协议框架

预处理：Prover 和 Verifier 构造 $[q_{L} (X)]$ ， $[q_{R} (X)]$ ， $[q_{O} (X)]$ ， $[q_{M} (X)]$ ， $[q_{C} (X)]$ ， $[σ_{a} (X)]$ ， $[σ_{b} (X)]$ ， $[σ_{c} (X)]$

第一步：Prover 针对 $W$ 表格的每一列，构造 $[w_{a} (X)]$ ， $[w_{b} (X)]$ ， $[w_{c} (X)]$ ， $ϕ (X)$ 使得

$q_{L} (X) w_{a} (X) + q_{R} (X) w_{b} (X) + q_{M} (X) w_{a} (X) w_{b} (X) - q_{O} (X) w_{c} (X) + q_{C} (X) + ϕ (X) = 0$

第二步： Verifier 发送随机数 $β$ 与 $γ$ ；

第三步：Prover 构造 $[z (X)]$ ，使得

$L_{0} (X) (z (X) - 1) z (ω \cdot X) g (X) - z (X) f (X) = 0 = 0$

第四步：Verifier 发送随机挑战数 $α$ ；

第五步：Prover 计算 $h (X)$ ，并构造商多项式 $[t (X)]$

$h (X) = q_{L} (X) w_{a} (X) + q_{R} (X) w_{b} (X) + q_{M} (X) w_{a} (X) w_{b} (X) - q_{O} (X) w_{c} (X) + q_{C} (X) + ϕ (X) + α (z (ω X) \cdot g (X) - z (X) \cdot f (X)) + α^{2} (L_{0} (X) \cdot (z (X) - 1))$

其中

$f (X) g (X) = (w_{a} (X) + β \cdot i d_{a} (X) + γ) (w_{b} (X) + β \cdot i d_{b} (X) + γ) (w_{c} (X) + β \cdot i d_{c} (X) + γ) = (w_{a} (X) + β \cdot σ_{a} (X) + γ) (w_{b} (X) + β \cdot σ_{b} (X) + γ) (w_{c} (X) + β \cdot σ_{c} (X) + γ)$

其中商多项式 $t (X) = \frac{h ( X )}{z _{H} ( X )}$ ；

第六步：Verifier 发送随机挑战数 $ζ$ ，查询上述的所有 Oracle，得到

$\overset{w}{ˉ}_{a} = w_{a} (ζ)$ ， $\overset{w}{ˉ}_{b} = w_{b} (ζ)$ ， $\overset{w}{ˉ}_{c} = w_{c} (ζ)$
$\overset{q}{ˉ}_{L} = q_{L} (ζ)$ ， $\overset{q}{ˉ}_{R} = q_{R} (ζ)$ ， $\overset{q}{ˉ}_{M} = q_{M} (ζ)$ ， $\overset{q}{ˉ}_{O} = q_{O} (ζ)$ ， $\overset{q}{ˉ}_{C} = q_{C} (ζ)$
$\overset{σ}{ˉ}_{a} = σ_{a} (ζ)$ ， $\overset{σ}{ˉ}_{b} = σ_{b} (ζ)$ ， $\overset{σ}{ˉ}_{c} = σ_{c} (ζ)$
$\overset{z}{ˉ}_{(ω \cdot ζ)} = z (ω \cdot ζ)$ ， $\overset{z}{ˉ}_{(ζ)} = z (ζ)$
$\overset{ˉ}{t} = t (ζ)$

Verifier 还要自行计算

$\overset{ˉ}{f}_{(ζ)} = (\overset{w}{ˉ}_{a} + β \cdot ζ + γ) (\overset{w}{ˉ}_{b} + β \cdot k_{1} \cdot ζ + γ) (\overset{w}{ˉ}_{c} + β \cdot k_{2} \cdot ζ + γ)$
$\overset{g}{ˉ}_{(ζ)} = (\overset{w}{ˉ}_{a} + β \cdot \overset{σ}{ˉ}_{1} + γ) (\overset{w}{ˉ}_{b} + β \cdot \overset{σ}{ˉ}_{2} + γ) (\overset{w}{ˉ}_{c} + β \cdot \overset{σ}{ˉ}_{3} + γ)$
$L_{0} (ζ)$
$z_{H} (ζ)$
$ϕ (ζ)$

验证步：

$\overset{q}{ˉ}_{L} \overset{w}{ˉ}_{a} + \overset{q}{ˉ}_{R} \overset{w}{ˉ}_{b} + \overset{q}{ˉ}_{M} \overset{w}{ˉ}_{a} \overset{w}{ˉ}_{b} - \overset{q}{ˉ}_{O} \overset{w}{ˉ}_{c} + \overset{q}{ˉ}_{C} + ϕ (ζ) + α (\overset{z}{ˉ}_{(ω \cdot ζ)} \cdot \overset{g}{ˉ}_(ζ) - \overset{z}{ˉ}_{(ζ)} \cdot \overset{ˉ}{f}_{(ζ)}) + α^{2} (L_{0} (ζ) \cdot (\overset{z}{ˉ}_{(ζ)} - 1)) = ? \overset{ˉ}{t} \cdot z_{H} (ζ)$

ZKPunk's ZKPedia