Thanks
- 感谢SecbitLabs @郭宇 前两个月分享的Spartan Overview (尽管当时也没太理解), 以及@even 在研究方向上的指引(据说Hyrax 不太好啃),不至于走太多弯路。
Motivation
缘于folding,缘于NOVA,缘于Setty,了解到了Spartan,但并不认识它,所以才有了本篇及接下来的关于它的一切(预备知识)……
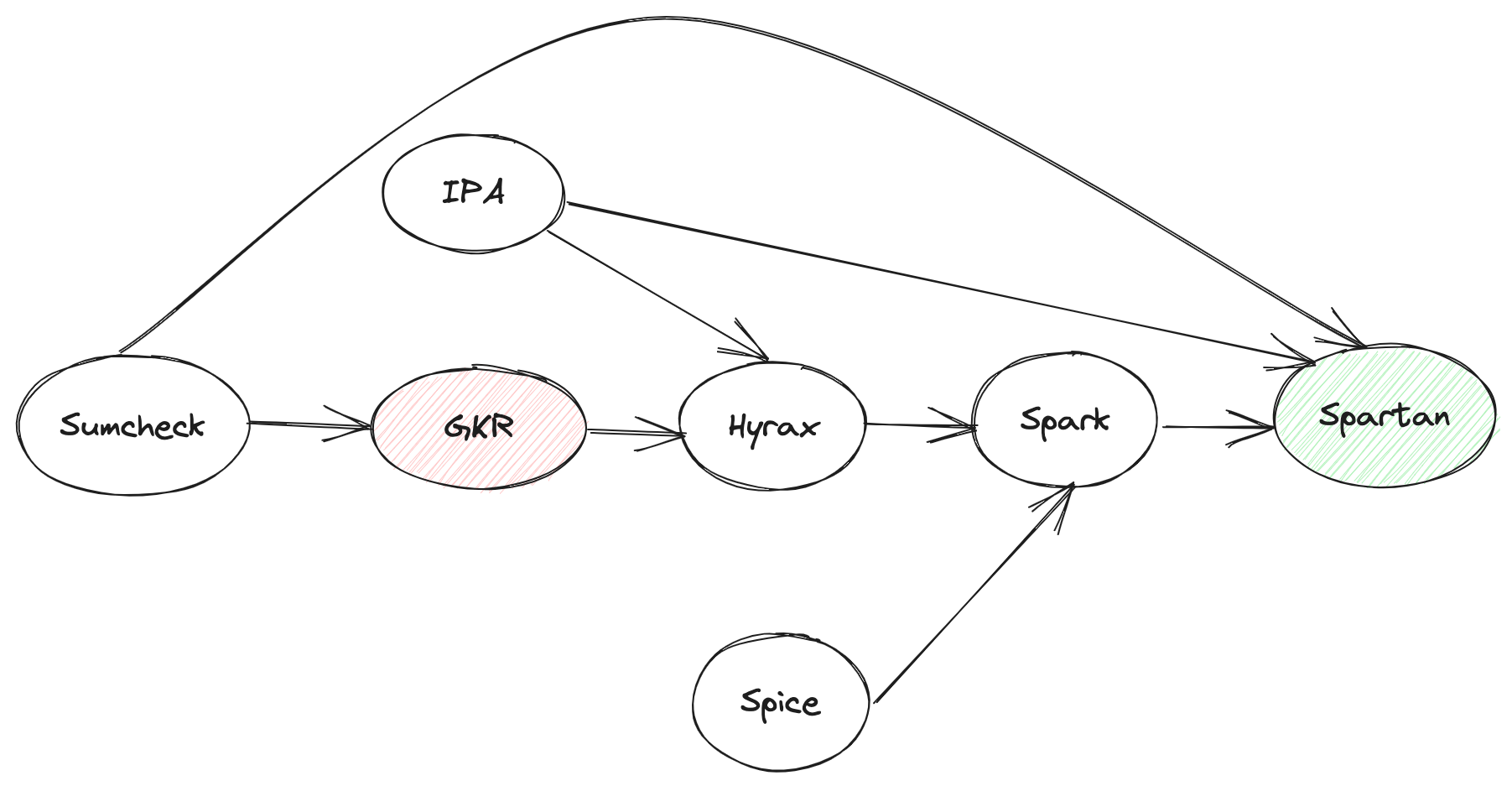
关于Spartan,在ZK领域可能时间上相对也有点儿远了,暂且不考虑它在某些方面的争议,它的一些思想其实已经影响到其它比较热门的方向了,比如当下的热点Lasso & Jolt,所以它的研究意义仍然很大。
Overview
- 本篇文章主要参考Hyrax 论文后半部分5-6节,即Hyrax 基于GKR with ZK Argument的contribution。
- 主要分为两部分,前半部分Reduced Sumcheck Verification主要针对GKR with ZK Argument的Step Two做的优化,对应Hyrax 论文中的Part 5。
- 后半部分Reduced Witness Evaluation 主要针对GKR with ZK Argument的Final Step做的优化,对应Hyrax 论文中的Part 6。
- 为了方便对照原始论文理解,本文中的notion尽量与Hyrax 原始论文对齐。
Reduced Sumcheck Verification
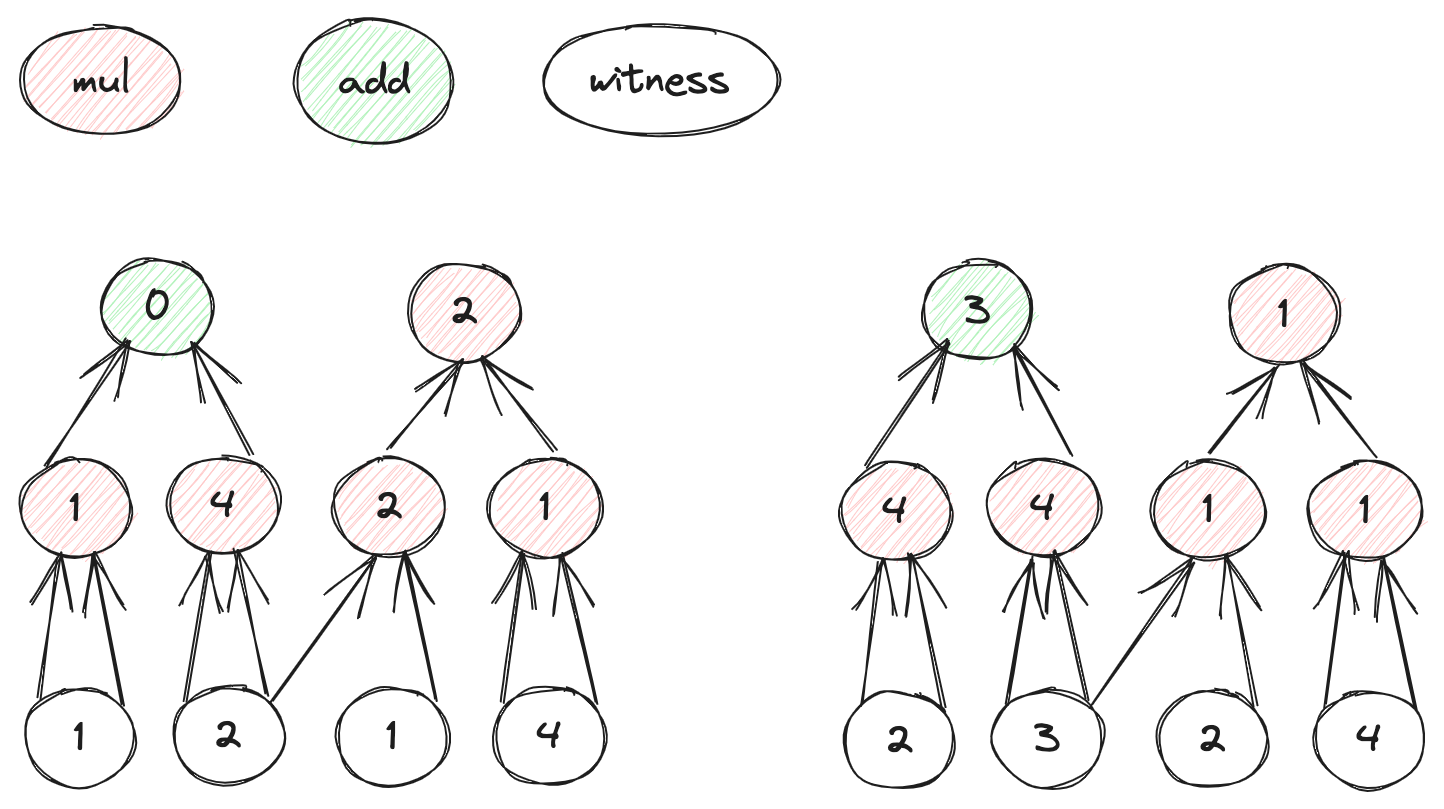
仍然以这个图为例,,则;第0层,,则;第1层,,则;第2层,,则。
Number of Sumcheck Commitments
为了简单起见,上一篇GKR with ZK Argument 中Sumcheck 协议每次round prover 发送给verifier 的多项式系数的commitment的个数我们固定都是4,也就是说多项式的degree全为3。其实prover 需要commit的多项式的degree是有变化的。
当round 时,prover commit的多项式的degree为3,也就是说commitment的个数为4:
当round 时,prover commit的多项式的degree为2, 也就是说commitment的个数为3:
Sumcheck Verifications
我们试图把verifier sumcheck 协议中所有round的校验等式且一个矩阵点乘运算表示:
其中每个round prover发送的message 为:
把它们聚合到一个向量里:
其中每个round verifier 需要验证时用的参数:
把它们聚合到一个矩阵里:
每一个round verifier 校验的结果:
备注:其中, 是第1个round 需要校验的sumcheck 值,是verifier 随机采样的第0层电路编码的evaluation值,也是prover 第1个round要证明的值。
汇总一下就是:
矩阵 需要verifier 自行计算,用红色标记的向量 和 向量 都是需要prover 进行commit。 如果说仍然是一个field对应一个commitment,那么commit之后的校验就变成了:
有没有觉得向量 size太大了(19个commitment)?是的,它直接影响着协议过程中的communication cost,所以需要进行压缩处理。
Reducing Sumcheck Commitments
一个field 对应一个commitment: 每次commit的时候还需要一个blind factor .
这样的话Sumcheck 协议中的commitment个数就会与要commit的多项式的degree成线性关系。如果把一个多项式所有参数的commitment压缩成一个commitment:
这样的话就需要多个generator 了,但blind factor 变成了一个。
我们用矩阵第一行的校验为例:
如果把commitment 压缩成一个commitment ,verifier 就无法直接通过上面的等式来进行校验。这其实就转换成了大家所熟知的IPA 证明,即Inner Product Argument verification。 接下来简单描述一下IPA协议的执行过程
IPA Protocol Overview
prover 要证明query 向量 满足:
Step One
prover 生成多项式的commitment,并发送给verifier
Step Two
prover 采样一个与向量 等长的向量,对它进行commit;同样也与query 向量 交互,结果也进行commit,最后同样也发送给verifier
Step Three
verifier 发送一个challenge factor 给prover,prover 计算
并把它们全部发送给verifier。
Step Four
根据commitment 同态性质,verifier 验证:
Reducing Sumcheck into IPA
最后我们看看Hyrax 中Sumcheck 协议被reduced成IPA 协议后的执行过程:
Step One
把多个verification fold成一个:
对 进行commit:
对 进行commit:
commit 之后,prover要证明的变成了:
把两组commitment 和 全部发送给verifier。
定义 ,,即剔除掉最后三个元素,则:
Step Two
prover 随机生成一个与 等长的向量,同 一样计算它的commitment,及 的commitment:
把两组 commitment 和 全部发送给verifier。
Step Three
verifier 发送一个challenge factor 给prover,prover 计算:
Step Four
verifier 验证:
到此为止多个round 的Sumcheck verification就被转换成了一个IPA verification,proof size(commitments) 也被进一步压缩。
Reduced Witness Evaluation
Recall
GKR with ZK Argument协议的Final Step是要对最下面一层(input + witness) 的某个evaluation 进行证明,我们仍然用GKR with ZK Argument中的例子:
需要verifier基于Step ZERO发送过来的每个witness对应的commitment 计算witness MLE上的evaluation值对应的commitment:
它的问题在于,需要对每个witness进行commit(上面红色标记的部分),导致communication cost 和 verification cost都会比较高,与witness的长度成线性关系,Hyrax 对其进行了压缩,变成了子线性关系。
Square-root commitment scheme
Hyrax 在这里的整体思路是,把上面witness evaluation 的commitment的计算代理给了prover,prover 提供计算结果的同时需要提供相应的proof给verifier 验证,当然了verifier 验证的成本肯定要低于自己计算的成本,满足succinct 特性:
把witness evaluation 的commitment的证明最终变成了一个IPA 的证明。
实例中。
Evaluation and Proof
prover 把witness 向量转换成一个矩阵表示, 其中分别代表行和列:
按行进行commit:
把witness的commitment 连同evaluation 的commitment 一起发送给verifier。
Compressed Lagrange Basis
基于MLE 多项式:
我们把Lagrange Basis Polynomial 一拆为二:
结合上面的witness 矩阵, 一定有:
通过两组的子向量来represent 长度为的整个向量,这里应该是一种很常见的succinct 做法。比如protostar 论文中3.5 节compressed verification也是采用了这种技巧,细节可以参考 https://learnblockchain.cn/article/6503
所以verifier 需要自己计算拿到两个向量(为了简化,实例中,所以其实是没有起到compress作用的,如果compress 效果就出来了,读者可以自行举例):
并计算得到: 其中 为commitment, 为verifier 刚计算好的scalar,最终verifier 拿到一个commitment 。
IPA for Evaluation Verification
最终verifier 需要对prover 提供的evaluation的commitment进行验证,这时的验证就变成了标准的IPA 验证:
关于IPA 的执行过程这里就不再赘述了,可以参考上面的IPA Protocol Overview。
Summary
到此,Hyrax 协议也就完整了。简单总结一下,Hyrax 本质就是一套GKR 协议,它在proof size 和 verification 方面做了一些工作。
References
【1】Hyrax 论文:https://eprint.iacr.org/2017/1132.pdf
【2】PAZK by Thaler:https://people.cs.georgetown.edu/jthaler/ProofsArgsAndZK.pdf
【3】protostar compressed verification: https://learnblockchain.cn/article/6503