- 作者:Maksym Petkus
- 翻译 & 注解:even@安比实验室([email protected])
- 校对:valuka@安比实验室
- 本系列文章已获作者中文翻译授权
- 翻译原链接
- Construction Properties
- Example Computation
- Verifiable Computation Protocol (可验证计算协议 )
- 2 security considerations
- 变量非延展性和变量一致性多项式
- 变量值一致性检查的优化
Construction Properties
Constant Coefficients 常量系数
在上文的构造中,我们通过对 未赋值的变量多项式 (unassigned variable polynomials) 的计算得到 0 或者 1 ,以此表示在运算中是否要用到这个变量。自然地想,我们也可以使用其它系数值,包括负数值,因为我们可以插值计算出经过任何必要的点(前提是没有两个计算使用了同一个 )的多项式。如下是这种运算的一些例子:
现在我们的程序就可以使用常量系数了,例如:
Algorithm 2: Constant coefficients
————————————————————————————————————————————————————————————
function calc(w, a, b)
if w then
return 3a × b
else
return 5a × 2b
end if
end function
在 阶段这些系数类似于 0 或者 1 将被“硬编码”进去,之后就不能再修改了。现在我们将运算形式修改为:
或者用更正式的参数 表示:
表示变量在运算中的位置 (左/右/输出)
Addition for Free (0 成本做加法)
看一下这个新结构,很显然在多项式的表示中,每一个不同 所要代表的操作数都是所有 操作数变量多项式(sum of all operand variable polynomials ) 的总和,其中只有一个被用到的变量是非零值而其它都为 0,下图就很好得表达了这个意思:
 我们可以利用这一个结构,加任何数量必要的 _变量_ 到每一个运算的操作符/输出中。例如在第一个运算中,我们可以首先做加法 _a+c_,然后就只需要用别的操作数与之相乘了,即 ,可以表示为下图:
我们可以利用这一个结构,加任何数量必要的 _变量_ 到每一个运算的操作符/输出中。例如在第一个运算中,我们可以首先做加法 _a+c_,然后就只需要用别的操作数与之相乘了,即 ,可以表示为下图:
 因而也可以将这些变量中任意个,对它们先乘以任意的系数 , 再一并加入到一起作为单个操作数中,以此来根据相应程序的需要构造一个操作数值。这个特性实际上就允许将运算结构改为:
因而也可以将这些变量中任意个,对它们先乘以任意的系数 , 再一并加入到一起作为单个操作数中,以此来根据相应程序的需要构造一个操作数值。这个特性实际上就允许将运算结构改为:
或者更正式一些用变量 和操作数变量系数
这个结构就是:
_注意 :每一个运算的操作数都有自己的一组系数 这里 乘法运算是关键,而加法运算都可以被合并到一个更大的乘法运算里面。
Addition, Subtraction and Division
到目前为止,我们一直专注于乘法操作。但是为了能够执行通用计算,真实环境下的程序也需要加法,加法和除法。
加法 前面我们确定: 可以在单个操作数的内容中将变量加起来,然后和另一个操作数相乘 —— 即 ,但是如果我们只是想做加法,没有乘法,例如一个程序中需要做 的计算,我们可以按照下面的方式来表示:
为什么强行 × 1 呢?
因为我们的结构中对于每一个操作数, 我们既需要常量系数也需要变量
1这个值可以表示为 ,其中 可以被“硬编码”到对应的多项式中, 是一个变量可以给它分配任何值,那么我们就必须通过一些约束来限制 的值,这个在后面的章节中将会讲到
减法 减法与加法几乎一致,唯一的不同就是负系数, 也就是:
除法 如果我们检查除法运算
可以看到除法的结果是就是我们要得到一个结果值使其乘以 divisor 能够得到 factor 。所以我们也可以用乘法来表示出同一个意思:divisor × result = factor . 这样就是说如果我们想要去证明除法运算 ,我们就可以把它表示为:
运算的结构也称为 “约束” ,因为多项式结构代表的运算,并非是为了计算出结果,而是在 prover已经知晓的变量赋值的情况下,检验这个运算的过程是否正确。换句话说,即约束 prover 必须提供一致的值,无论这些值是什么。
所有的算术计算(加减乘除)都已经有了,于是运算结构不再需要修改。
even@安比实验室: 约束和运算有一定的关联性。算术电路的目的是为了实现「计算的验证」,而非「计算的过程」。
上一篇文章中,我们提出了一种方法:把构造多项式的工作交给 环节, 只要填上对应的数值就可以了。 这个方法不仅解决了同一个操作数运算符中不一致的问题,同时还带来了额外的便利:
1) 允许执行计算的表达式中包含静态系数。 2)虽然 的关系中只有乘法,但利用这个方法也可以轻松的执行加法操作,继而也就解决了减法和除法的问题
Example Computation
看不太懂上面说啥, 直接看例子吧 !!
有了一组通用的运算结构,我们就可以将我们原始的程序转换成一组运算,然后再转换成多项式的形式。我们先来想一下算法的数学形式(用变量 表示运算结果): 这里有三个乘法,但是由于运算结构只支持一个乘法操作,所以这里至少就要做三次运算。我们先将它简化 :
-
<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6667em;vertical-align:-0.0833em;"></span><span class="mord mathnormal" style="margin-right:0.02691em;">w</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="color:green;">a</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin" style="color:green;">×</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="color:green;">b</span><span class="mclose">)</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.6667em;vertical-align:-0.0833em;"></span><span class="mord mathnormal" style="color:blue;">a</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin" style="color:blue;">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.7778em;vertical-align:-0.0833em;"></span><span class="mord mathnormal" style="color:blue;">b</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.6667em;vertical-align:-0.0833em;"></span><span class="mord mathnormal" style="margin-right:0.02691em;">w</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="color:green;">a</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin" style="color:green;">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="color:green;">b</span><span class="mclose">)</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span></span></span></span>
写出 :
第 3 条是增加的约束使 必须为二进制,否则 就可以代入任何值去执行恶意运算
现在一共有 5 个变量 ( 2 个左操作符 , 4 个右操作符 和 5 个输出 ) , 操作符多项式为:
在在三次运算中, 必须为每个变量多项式 都分别算出一个对应的系数, 或者如果这个多项式在计算的操作数或者输出中没有被用到的话, 系数就置为 0 :
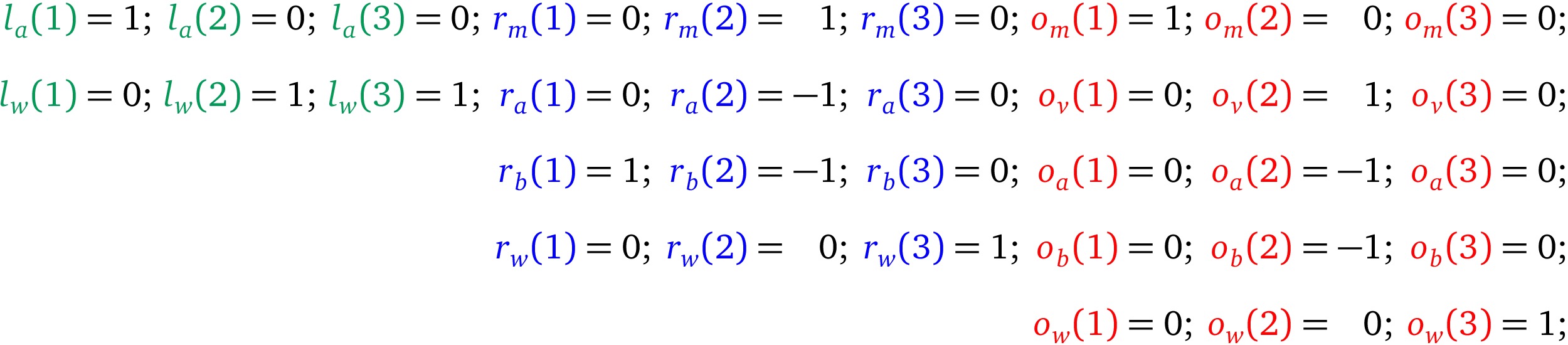 如上图
如上图
- 对于左操作数 : a 在第 1 行约束出现, 所以 , w 在第 2/3 行约束出现, 所以 ,
- 对于右操作数 : 注意 第 2 行约束的
因为有三行约束, 所以 target poly 就是
Next we leverage polynomial interpolation to find each variable polynomial :
- …
绘制出来就是:

OK! Now we are ready to prove computation through polynomials.
首先,选择函数的输入值,例如: 。其次,计算过程中的中间变量值为:
然后,我们把所有计算结果中的值赋值到 变量多项式 (variable polynomial) 中,然后相加得到操作数或者输出多项式的形式:
注意: 的系数是其赋值, 比如 的系数都是
1, 的系数都是3… 的系数则是2×3 => 6
在图中就表示为:

上图表示的, 就是 上上图 里的 等都被 “拉长了” , 拉长成了
把他们具体组合成 , 即相加对应操作数如 …
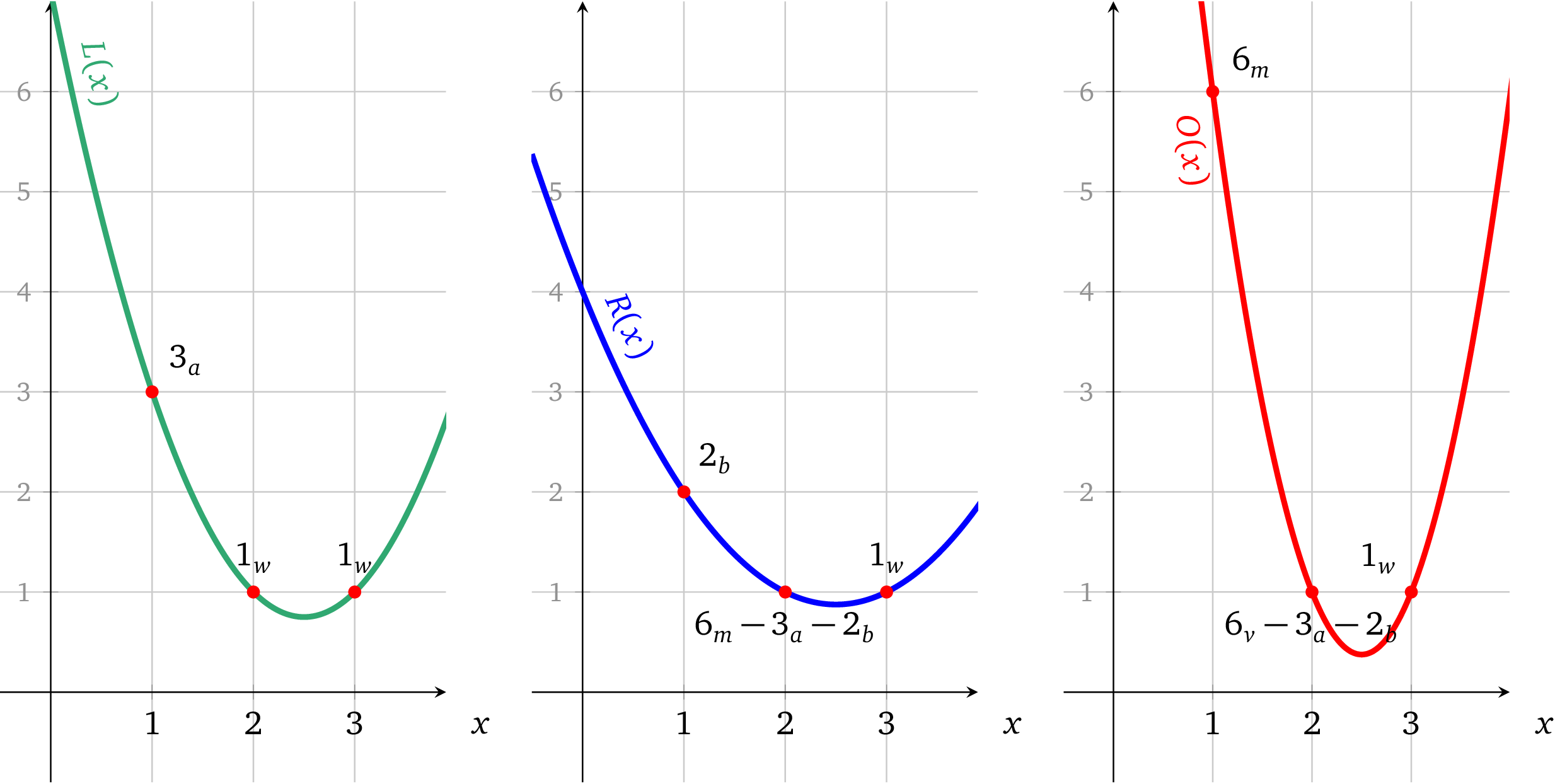
Recap 上图: :
- 经过了
- 经过了
- 则 经过了
表示给 这个变量赋值为 2
我们需要去证明 ,因而我们先 长除法 找出 :
以图的形式表示为:
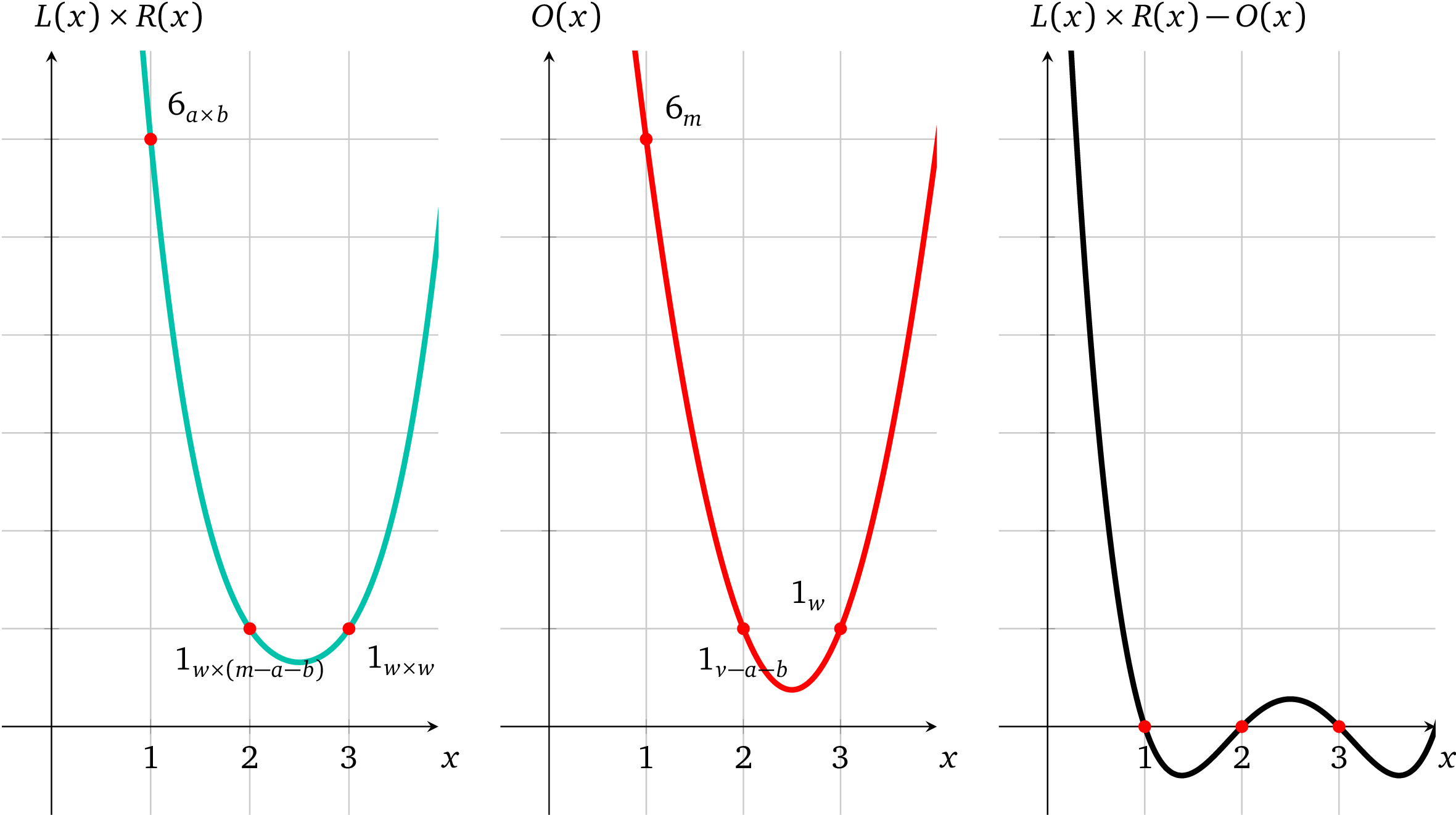
图示很明显, 多项式 有根为 : ,因而 是它的因式,假如使用了和它不一致的变量值,情况就不是这样了
这就是一组能够正确计算的变量值,如何在多项式层面上证明出来的。下面 还要再继续处理协议的密码学部分
Verifiable Computation Protocol (可验证计算协议 )
我们基于前文中多项式知识协议 做了很多修改使它变得更通用 (general-purpose),来看一下它现在的定义
假设约定函数 f(*),约定其计算结果为证明对象(proof),其次数为 ,变量数为 ,其对应的系数:
Setup :
- 为左操作数 (类似 ) 构造变量多项式(variable polynomial) 然后对于所有 的运算都算出其对应的系数,即 , 对右操作数和输出也做同样的事情。 这样的
- 随机抽取
- 计算 及
- 计算 proving key:
- 计算 verification key :
Proving :
- compute function
f(*)and therefore corresponding variables values- 我理解这里就是 个变量 每个变量的赋值即 witness
- 计算 ,其中 , 也是类似处理
- 给 个变量赋值 求和, 得到 operand poly :
- assign variable values to the shifted poly :
- 使用 的幂加密值: 计算加密值 给
- set proof
Verification :
- parse proof as
variable polynomialrestriction check (要符合α-shifted)- valid operation check (计算结果的有效性)
The set of all the variable polynomials for and the target polynomial is called a quadratic arithmetic program (QAP, introduced in Gen+12 ).
虽然协议足够健壮,可以进行常规的计算验证,但这里依然还有两个安全考虑需要去解决。
2 security considerations
1 | Non-Interchangeability of Operands and Output
操作数和输出的不可替代性
Because we use the same for all operands of variable polynomials restriction check , there is nothing that prevents from
- 使用其它的操作数中的可变多项式,即
- 完全交换操作数多项式, 也就是把 和 换成
- 复用相同的操作数多项式,即
可交换性就是指 可以修改计算过程,并有效证明一些其它无关的计算结果。防止这种行为的一个很显然的方式就是在不同的操作数上使用不同的 ,具体协议就可以修改为:
选择随机数 来代替
Setup :
- sample random instead of
- calculate corresponding
shifts - Proving key : Proving :
- …
- assign variables to the shifted poly :
It is now not possible to use variable polynomials from other operands since following
α-sare not known to the prover: (这样就不能在一个操作数中使用其它操作数(operands) 的变量多项式了,因为prover没有办法去获知 来满足 变换关系 )
even@安比实验室: 这里通过对 和 进行分开 KEA 检查,就解决了上篇文章中提出的第二个缺陷问题——由于 prover 生成的证明中只有计算结果,左操作数,右操作数,输出在计算中混用也不会被发现。
同样下面一节也解决了上篇文章中提出的第三个缺陷问题——由于左操作数,右操作数,输出是分开表示的,互相之间的关系无法进行约束
2 | Variable Consistency Across Operands(一致性校验和)
跨操作数的变量一致性
For any variable we have to assign its value to a variable polynomial for each corresponding operand, i.e.: ( 对于任意的变量 ,我们都必须将它的值 分配 到每个相应操作数中的一个与之对应的 变量多项式 上,即:) Because the validity of each of the operand polynomials is checked separately, no enforcement requires to use same variable values in the corresponding variable polynomials. This means that the value of variable in left operand can differ from variable in the right operand or the output. ( 因为每一个 operand polynomials 的有效性是分开校验的,并不强制要求我们在对应的 variable polynomials 中使用相同的变量值。这就意味着在左操作数中变量 的值可以与右操作数或输出中的变量值 不同)
我们可以通过熟悉的限制多项式的方法(也就是限制变量多项式的方法)在操作数之间强制变量值相等。
If we can create a “shifted checksum” variable polynomial across all operands, that would restrain prover such that he can assign only same value. A verifier can combine polynomials for each variable into one, e.g.,
( 如果我们能够在所有的操作数之间创造一个作为“变换的校验和”(shifted checksum) 的变量多项式(variable polynomial),(这里我理解就是创建一个包含了所有 variable 的 variable poly, 对这些所有的 variable 整体做 α-shift, 就一个都别跑都被约束住了) 那么就可以限制 使其只能够赋予(给每个变量)相同的值。 可以将这些每个变量的多项式加起来,即:
然后乘以一个额外的随机数 β ,即
提供这些 β-shifted poly 给 ,与变量多项式一起给它赋上变量值:
然后加密 β 并把 加到 verification key 中。现在如果所有的 值相同,即,
等式就满足:
(2) 式的底 被暂时忽略省去了
如上, 式成立的条件是 : 当且仅当 都相等时,这个等式才会成立
尽管这个一致性校验很有用,但还是存在一定的概率 中至少有两项要么计算值相同, 要么一个多项式可以被另一个整除等情况,这就允许 去分解 这些值的关系,使得即使有至少两个不相等的值也依然能够保持等式成立,从而使上 式的校验无效
例如,一个以 为例的单个运算。我们用 w 来表示这 2 式的评估, 同时令 。这个等式看起来就是:
对于任意的 和 ,这种形式可以令 ,上式也就变换成: 所以说, 如果 刻意让 , 则这样的一致性策略是恒成立/无效的。缓解这种情况的一种方法是对每个操作数都使用不同的 , 确保操作数的 变量多项式 中包含无法预测的值
以下是修改后的协议:
Setup
-
…随机数
-
对 variable consistency poly(变量一致性多项式) 进行计算,加密并添加到
proving key中: -
对 加密并将其加到 verification key 中:
Proving
- …assign variable values to variable consistency poly :
- add assigned polys in encrypted space : (将赋值的多项式加
加密空间中):- 对每一个变量 ,都要计算它的一致性校验和(shifted-checksum) ,然后我们将所有的 的值相乘, 得到
- add to the proof:
在这后面增加吗?
Verification
- …校验提供的 操作数多项式 和 “校验和”多项式之间的一致性: PS: Pairing 公式参考 :
这个构造中, 同一个变量值就无法乱用了,因为不同的 使得相同多项式无法兼容,但是这里还存在与 remark 4.1 相同的缺陷,由于 是公开可见的, 攻击者可以修改任意变量多项式的零索引系数(modify the zero-index coefficient of any of the variable polynomials),因为它并不依赖于 ,i.e.
变量非延展性和变量一致性多项式
(Non-malleability of Variable and Variable Consistency Polynomials)
1 | 变量多项式的延展性
Recall 第三章的 Remark 4.1 : 可以在操作数多项式上分配一个 ,而 不能检测到 , 下面具体描述了 对多项式进行特定加(或减)操作的能力,而这种操作不会影响 配对验证 , 因而可以修改多项式使其超出 的预期或 prove a different statement,后面的章节我们将会解决掉这个问题 : 由于 verification key 中包含了加密了的 : , 所以 可以用多项式加(或者减)任意一个值 而不会破坏 Pairing 的成立. 后面我们会解决掉这个 bug
举一个 remark 4.1 有关的例子,看一下下面的两个运算: 预期的结果 b = a 和 c = 3a , 即 c = 3b。这就是说 left operand’s variable polynomial 的计算结果为 和 (第 行约束的系数为 , 第 行的约束为 )
先不管 的形式, 都可以不按照上述的比例用另一个修改了的多项式 来给 赋值。这样运算就变成了 和 , 结果也就是 b = a + 1 和 c = 3a + 1,其中 c ≠ 3b ,这意味着 的取值的实际意义在不同运算中是不一样的
但是因为 已经拿到了 和 ,所以他依然能够正确地通过 correct operand polynomials 和 variable values consistency 的校验:
…Proving:
- 用分配不成比例的变量 a 来建立左操作数多项式:
- 按照常规的方式构造右操作数多项式和输出多项式:
- 计算除数:
- 计算加密值: ,并按照常规方式计算
- 计算 α-shifts 的加密值: ,并按照常规方式计算
- 计算变量一致性多项式:
其中下标 代表对应变量的符号, 指数 代表变量的值;以及未定义的变量多项式的值为 0。
- set proof :
Verification:
-
variable poly restriction check : and as usually for
-
变量多项式约束检查:
-
有效计算检查:
2 | Malleability of Variable Consistency Polynomials(变量一致性多项式的延展性)
Moreover, allows to use different values of same variable in different operands. For example, if we have an operation:
(而且 的存在允许我们在不同操作数的相同变量上使用不同的值。例如,如果我们有一个运算):
Which can be represented by the variable polynomials: 简单插值, 得到 尽管我们期待的输出是 ,但我们可以设置不同的 值,例如:设置 (left operand), (right operand) , 如下:
Proving:
- …用 设置左操作数多项式
- 用 设置右操作数多项式
- (在 时) , 所以
+3是为了确保我们在 处得到正确的操作数 5
- (在 时) , 所以
- 用 设置输出多项式 :
- … 计算加密值 :
- 计算变量一致性多项式: Verification:
- ……变量值的一致性检查,应满足:
注意:多项式 其实可以被忽略掉的,因为这几项对于任何 的取值,计算结果都为 0,但是为了保持完整性我们依然要保留这几项
even@安比实验室:这种能力会危害到协议的可靠性。很显然,加密的 不应该对 Prover 可见
3 | Non-Malleability 非延展性
解决延展性(Malleability) 问题的一个方法就是,在 setup 阶段将 encrypted space中的 项与随机秘密值 (gamma) 相乘, 从而使 verification key 中加密的 与加密值 不兼容: 相应的这种被修饰过的加密值,就能阻止修改加密值 的可行性,因为 中没有 ,即:
注 :
因为变值 是随机的, 并不知道它的值。所以这个修改就需要我们用 乘以 来平衡协议中的变量值一致性校验等式:
Setup:
- …随机数
- …设置 verification key: Proving: … Verification:
- … 变量值一致性检查应满足: 这里很重要的一点是我们排除了变量多项式为 0-阶的例子(e.g. ),否则就可以从 proving key 的 variable consistency polynomials (变量一致性多项式) 中揭露出加了密的 值 比如这个例子中当操作数(Operand) / 输出(Output) 中的任意两项为 时, e.g. , this will result in : 如此 就直接被 exposed 出来了
我们同样也可以通过“修饰“(mask) α-s 项来解决 变量多项式 的延展性问题。但是这就没有必要了,因为对于 变量多项式 的任何修改,都需要被映射到变量的 一致性多项式 中,而一致性多项式是无法修改的
变量值一致性检查的优化
现在 variable values consistency check 是有效的,但是这里在 verification key 中增加了 4 个昂贵的 Pairing 操作和 4 个新的项。文献 Par+13 中的 Pinocchio 协议用了一个很聪明的方法优化,通过选择不同的生成元 ,从而对每个 operand 实行“移位”:
Setup
- …选择随机值 , and set
- set generators
- set proving key:
- 设置 verification key:
Proving
- …assign variable values : Verification
- …变量多项式约束检查: & 对 做同样的检查
- 变量值约束检查:
- 有效运算检查:
生成元的这种随机化进一步增加了安全性,使得如 remark 4.1 中描述的 variable polynomials 延展性无效。因为对于故意的修改,它必须要么是 原始值的倍数 , 要么就是不可直接用的加密值的倍数(假定, 如上文所述我们不去处理可能曝光加密后的值的 0 阶可变多项式)
这个优化使得 verification key 减少了 2 个项, i.e. instead of : ,并且去除了 verification 步骤中的两个配对运算 :
注意:这在 Jens Groth 2016 年的 paper Gro16 中有更进一步的改进
even@安比实验室: 至此,通用 zk-SNARK 协议的已经几乎构造完成了,本文可以归纳为以下几点:
- 协议中是如何增加可变系数的和如何做加减乘除运算的
- 协议如何保证操作数和输出的不可替代性
- 协议如何保证跨操作数的可变一致性
- 协议如何处理非延展性变量和变量一致性
- 协议中变量值一致性检查优化
Reference :
- https://secbit.io/blog/2020/01/15/learn-zk-snark-from-zero-part-four/
- https://medium.com/@imolfar/why-and-how-zk-snark-works-5-variable-polynomials-3b4e06859e30
- https://medium.com/@imolfar/why-and-how-zk-snark-works-6-verifiable-computation-protocol-1aa19f95a5cc