- 感谢SecbitLabs @郭宇 前两个月分享的Spartan Overview (尽管当时也没太理解), 以及@even 在研究方向上的指引(据说Hyrax 不太好啃),不至于走太多弯路。
缘于folding,缘于NOVA,缘于Setty,了解到了Spartan,但并不认识它,所以才有了本篇及接下来的关于它的一切(预备知识)……
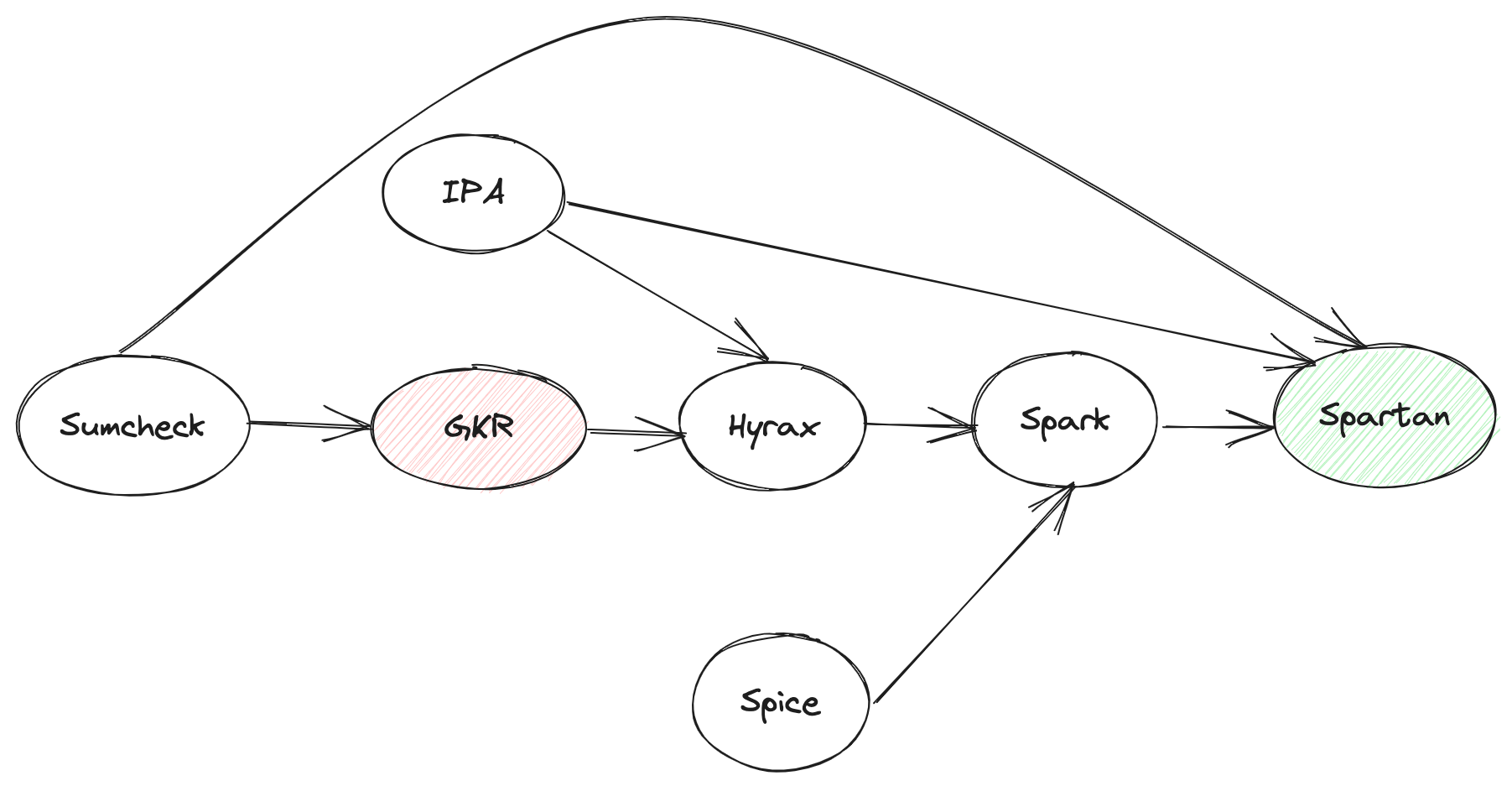
关于Spartan,在ZK领域可能时间上相对也有点儿远了,暂且不考虑它在某些方面的争议,它的一些思想其实已经影响到其它比较热门的方向了,比如当下的热点Lasso & Jolt,所以它的研究意义仍然很大。
- 本篇文章主要参考Hyrax 论文前半部分1-4节,即优化前的GKR zk argument
- GKR 协议本身是Sumcheck协议的一种应用,不带zk argument的GKR 就可以简单认为是多个sumcheck协议的叠加,带zk argument的GKR就会带来很多的细节问题,这也是Hyrax 的起源,所以弄清楚GKR with zk argument 的各个细节后自然也就清楚了Hyrax的意义
节选自PAZK 中的图
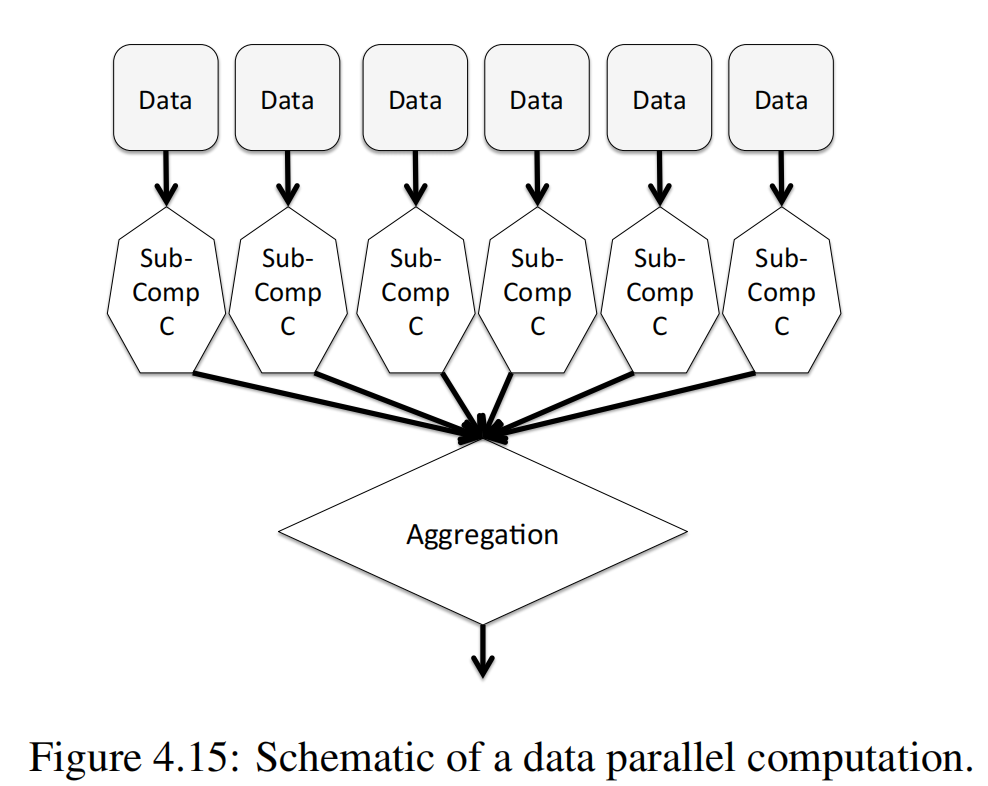
何为数据并行化GKR?就是同一个电路描述应用在多组input 数据中的GKR 协议,这样prover 在最开始的claims 中就不再是针对单一电路的output,比如下面的 V0=(0,2):
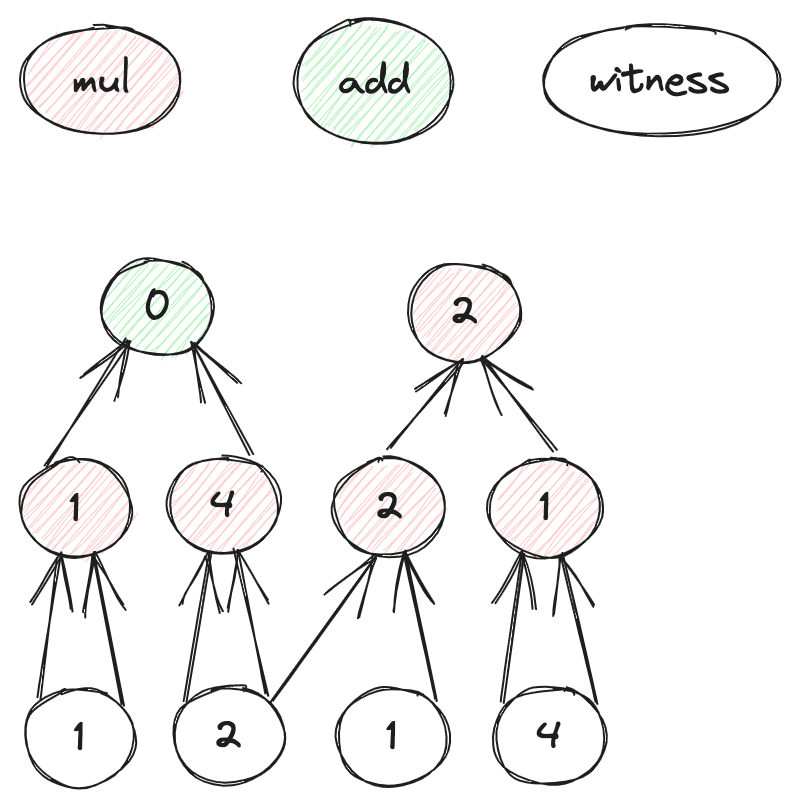
而是多个子电路的output的汇总 V0=(0,2,3,1):
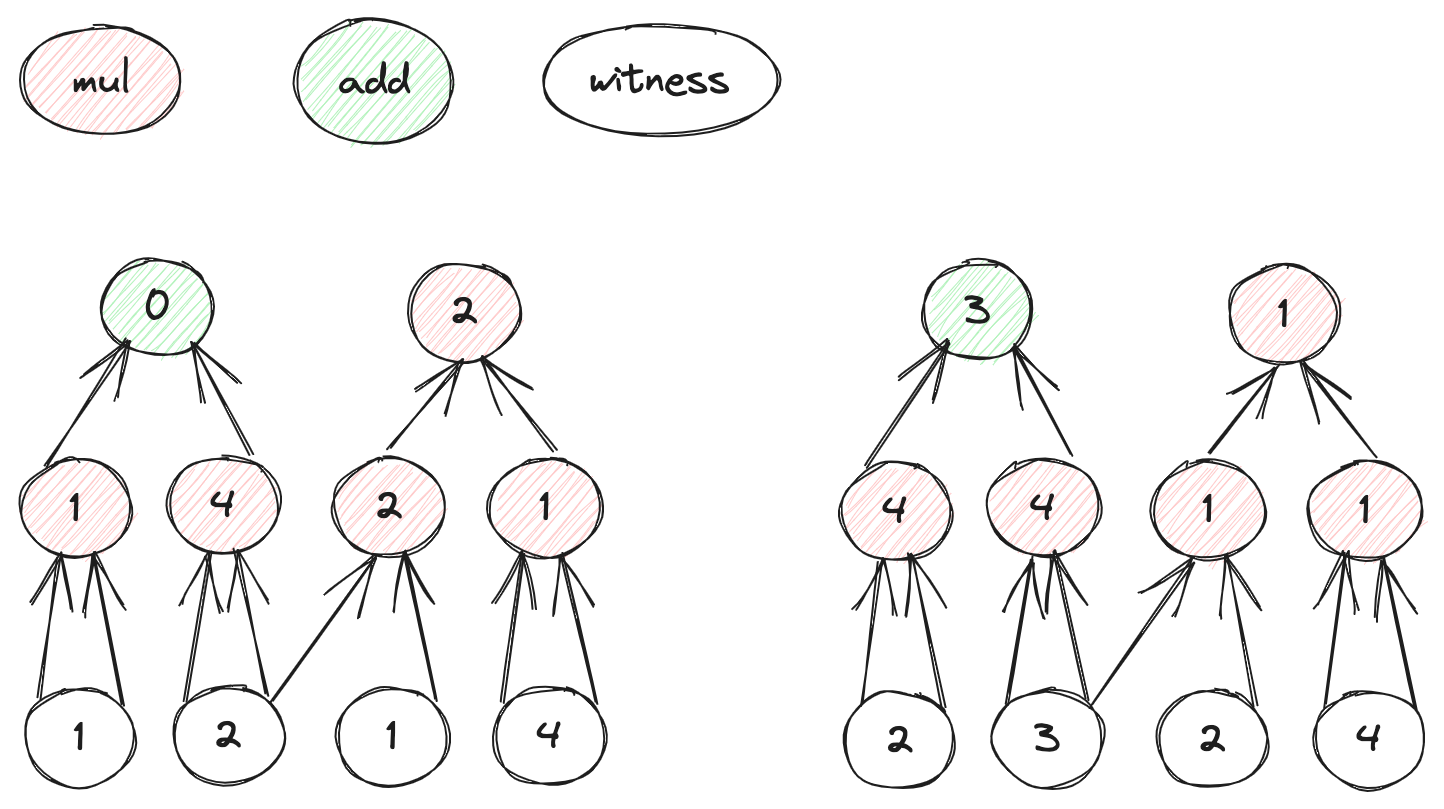
在GKR协议中prover 要证明也不再是:
Vi−1(q)=hL∈{0,1}bG∑hR∈{0,1}bG∑addi(q,hL,hR)(Vi(hL)+Vi(hR))+muli(q,hL,hR)(Vi(hL)⋅Vi(hR))
而是:
Vi−1(q′,q)Pq′,q,i(h′,hL,hR)=h′∈{0,1}bN∑hL∈{0,1}bG∑hR∈{0,1}bG∑Pq′,q,i(h′,hL,hR)=eq(q′,h′)⋅[addi(q,hL,hR)(Vi(h′,hL)+Vi(h′,hR))+muli(q,hL,hR)(Vi(h′,hL)∗Vi(h′,hR))]
另外需要备注一下各个notion的含义:
- Vi−1(q′,q) 代表第i−1 层电路编码q′∈FbN Gate编码q∈FbG 上的evaluation 值,Vi−1(q′,q)是Vi−1(q′,q)的MLE
- Vi(h′,hL)代表第i 层电路编码h′∈FbN Gate编码 hL∈FbG 上的evaluation 值,Vi(h′,hL)是Vi(h′,hL)的MLE;Vi(h′,hR)同理
- addi(q,hL,hR)和muli(q,hL,hR)分别代表{q,hL,qR}∈FbG上的加法和乘法Gate的MLE,注意Gate的描述与电路的编码q′∈FbN 无关,也跟input witness无关,所以它的计算可以在preprocessing 阶段就开始了,没有必要等到协议中才开始
- eq(q′,h′)代表电路编码q′∈FbN 与 电路编码h′∈FbN 是否一致,eq(q′,h′)是eq(q′,h′)的MLE
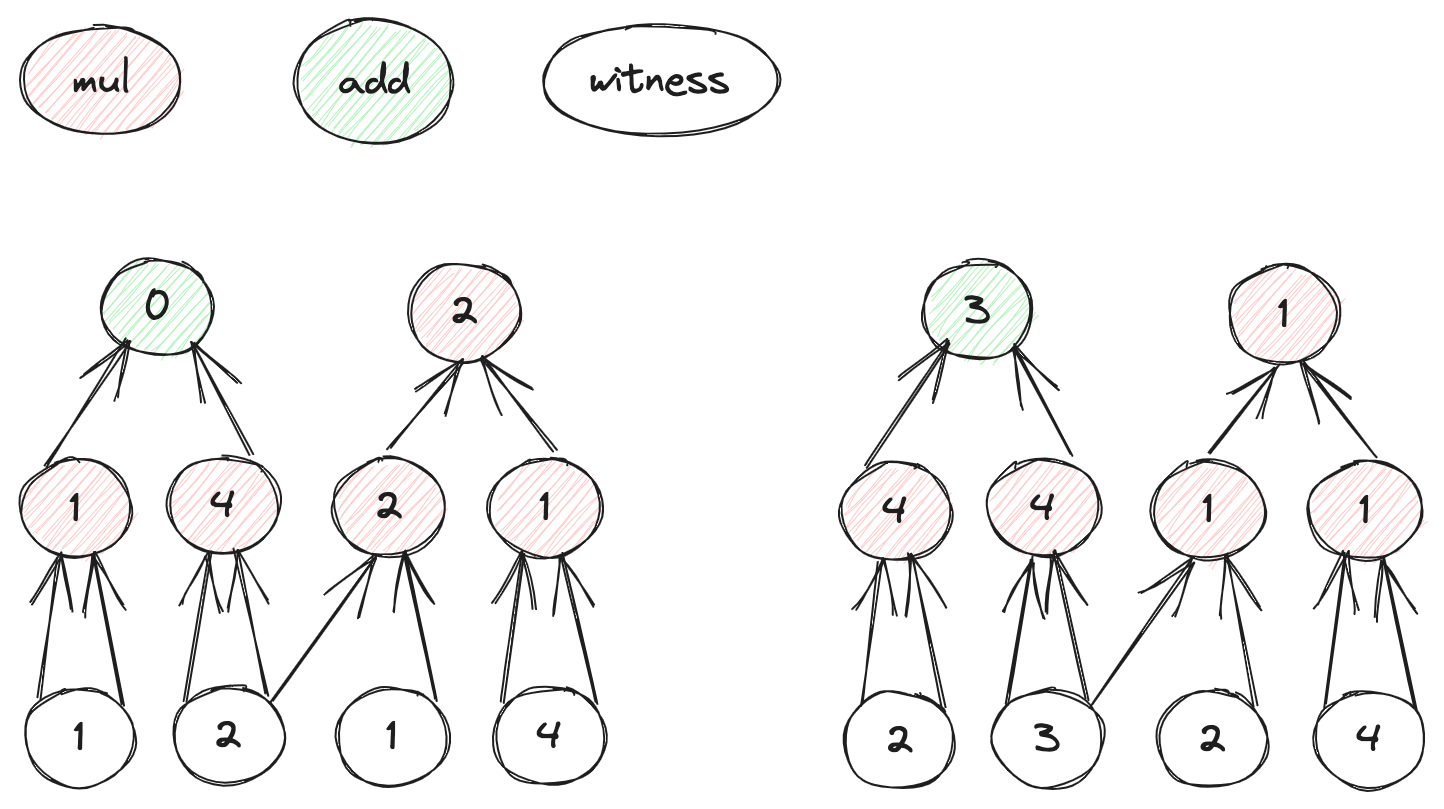
仍然以为个图为例来扮演整个协议的过程。其中电路的个数N=2,所以bN=1;有限域的moduler p=5。
假设前半部分为public input,后半部分为witness,对witness 的每个元素进行commit,并发送给verifier :
commit(2)、commit(3)、commit(2)、commit(4)
prover 发送电路的output 作为Sumcheck的初始claimsV0=(0,2,3,1),verifier 根据给定的电路第0层的evaluation 值:
bN0011bG0101V0(bN,bG)0231
可以插值出相应的多项式:
s0(x1,x2)=0⋅(1−x1)(1−x2)+2⋅(1−x1)x2+3⋅x1(1−x2)+1⋅x1x2
verifier 生成challenge factor(q′,q)=(2,4)=(x1,x2),并发送给prover,接下来进入第1层电路的 sumcheck 协议,prover 需要证明:
V0(q′,q)=h′∈{0,1}bN∑hL∈{0,1}bG∑hR∈{0,1}bG∑Pq′,q,1(h′,hL,hR)=h′∈{0,1}bN∑hL∈{0,1}bG∑hR∈{0,1}bG∑eq1(q′,h′)⋅[mul1(q,hL,hR)(V1(h′,hL)∗V1(h′,hR))+add1(q,hL,hR)(V1(h′,hL)+V1(h′,hR))]=?s0(2,4)=2
将第1层的sumcheck 多项式拆解成多个item :
eq1(q′,h′)mul1(q,hL,hR)add1(q,hL,hR)V1(h′,hL)V1(h′,hR)=eq1(2,y1)=2y1+(−1)(1−y1)=3y1−1=mul1(4,(y2,y3),(y4,y5))=4⋅y2(1−y3)⋅y4y5=add1(4,(y2,y3),(y4,y5))=(−3)⋅(1−y2)(1−y3)⋅(1−y4)y5=(1−y1)⋅[(1−y2)(1−y3)+4(1−y2)y3+2y2(1−y3)+y2y3]+y1⋅[4(1−y2)(1−y3)+4(1−y2)y3+y2(1−y3)+y2y3]=(1−y1)⋅[(1−y4)(1−y5)+4(1−y4)y5+2y4(1−y5)+y4y5]+y1⋅[4(1−y4)(1−y5)+4(1−y4)y5+y4(1−y5)+y4y5]
合并item :
V0(q′,q)]=V0(2,4)=h′∈{0,1}bN∑hL∈{0,1}bG∑hR∈{0,1}bG∑eq1(2,h′)⋅[mul1(4,hL,hR)⋅(V1(h′,hL)∗V1(h′,hR))+add1(4,hL,hR)⋅(V1(h′,hL)+V1(h′,hR))]=y1∈{0,1}∑y2∈{0,1}∑y3∈{0,1}∑y4∈{0,1}∑y5∈{0,1}∑(3y1−1)∗[(4y2(1−y3)y4y5)⋅[((1−y1)⋅((1−y2)(1−y3)+4(1−y2)y3+2y2(1−y3)+y2y3)+y1⋅(4(1−y2)(1−y3)+4(1−y2)y3+y2(1−y3)+y2y3))∗((1−y1)⋅((1−y4)(1−y5)+4(1−y4)y5+2y4(1−y5)+y4y5)+y1⋅(4(1−y4)(1−y5)+4(1−y4)y5+y4(1−y5)+y4y5))]+((−3)(1−y2)(1−y3)(1−y4)y5)⋅[((1−y1)⋅((1−y2)(1−y3)+4(1−y2)y3+2y2(1−y3)+y2y3)+y1⋅(4(1−y2)(1−y3)+4(1−y2)y3+y2(1−y3)+y2y3))+((1−y1)⋅((1−y4)(1−y5)+4(1−y4)y5+2y4(1−y5)+y4y5)+y1⋅(4(1−y4)(1−y5)+4(1−y4)y5+y4(1−y5)+y4y5))]
prover 计算本次round 验证需要用到的proof,也就是单变量多项式s1(y1):
y2y3y4y500011011f(y1)(3y1−1)⋅(−3)⋅((1+3y1)+4)(3y1−1)⋅4⋅(2−y1)
备注:y2y3y4y5 其它编码取值对应的多项式为0,就没有一一枚举出来
则:
s1(y1)=(3y1−1)⋅(−3)⋅((1+3y1)+4)+(3y1−1)⋅4⋅(2−y1)=2+2y1+y12=c0,1+c1,1y1+c2,1y12
prover 需要把多项式s1(y1)的commitment发送给verifier,也就是把该多项式的4个系数的commitment 之后发过去:
δc0,1=commit(c0,1)=commit(2)δc1,1=commit(c1,1)=commit(2)δc2,1=commit(c2,1)=commit(1)δc3,1=commit(c3,1)=commit(0)
verifier 需要验证:
s1(0)+s1(1)=?s0(2,4)=2
根据commitment 加法同态的性质,需要验证:
2δc0,1+δc1,1+δc2,1+δc3,1=?commit(s0(2,4))=commit(2)✓
验证通过,verfier 发送challenge factor r1=y1=3,下一个round 需要验证的目标值为:
s1(3)=2+6+9=17mod5=2
基于y1=3 ,prover 计算本次round 验证需要用到的proof,也就是单变量多项式s2(y2):
y3y4y5001011f(y2)8⋅−3(1−y2)⋅((10−11y2)+4)8⋅4y2⋅((10−11y2)∗1)
备注:y3y4y5 其它编码取值对应的多项式为0,就没有一一枚举出来
则:
s2(y2)=8⋅−3(1−y2)⋅((10−11y2)+4)+8⋅4y2⋅((10−11y2)∗1)=4+4y22=c0,2+c2,2y22
prover 需要把多项式s2(y2)的commitment发送给verifier,也就是把该多项式的4个系数的commitment 之后发过去:
δc0,2=commit(c0,2)=commit(4)δc1,2=commit(c1,2)=commit(0)δc2,2=commit(c2,2)=commit(4)δc3,2=commit(c3,2)=commit(0)
verifier 需要验证:
s2(0)+s2(1)=?s1(3)=2
根据commitment 加法同态的性质,需要验证:
2δc0,2+δc1,2+δc2,2+δc3,2=?commit(s1(3))=commit(2)✓
验证通过,verfier 发送challenge factorr2=y2=4给prover,下一个round 需要验证的目标值为:
s2(4)=4+64=68mod5=3
基于y1=3,y2=4,prover 计算本次round 验证需要用到的proof,也就是单变量多项式s3(y3):
y4y50111f(y3)8⋅9(1−y3)⋅((26y3−34)+4)8⋅16(1−y3)⋅((26y3−34)∗1)
备注:y4y5 其它编码取值对应的多项式为0,就没有一一枚举出来
则:
s3(y3)=8⋅9(1−y3)⋅((26y3−34)+4)+8⋅16(1−y3)⋅((26y3−34)∗1)=3+2y3=c0,3+c1,3y3
prover 需要把多项式s3(y3)的commitment发送给verifier,也就是把该多项式的4个系数的commitment 之后发过去:
δc0,3=commit(c0,3)=commit(3)δc1,3=commit(c1,3)=commit(2)δc2,3=commit(c2,3)=commit(0)δc3,3=commit(c3,3)=commit(0)
verifier 需要验证:
s3(0)+s3(1)=?s2(4)=3
根据commitment 加法同态的性质,需要验证:
2δc0,3+δc1,3+δc2,3+δc3,3=?commit(s2(4))=commit(3)✓
验证通过,verfier 发送challenge factorr3=y3=2给prover,下一个round 需要验证的目标值为:
s3(2)=3+4=7mod5=2
基于y1=3,y2=4,y3=2,prover 计算本次round 验证需要用到的proof,也就是单变量多项式s4(y4):
y51f(y4)8⋅−16y4⋅(18∗(4−3y4))+8⋅−9(1−y4)⋅(18+(4−3y4))
备注:y5 其它编码取值对应的多项式为0,就没有一一枚举出来
则:
s4(y4)=8⋅−16y4⋅(18∗(4−3y4))+8⋅−9(1−y4)⋅(18+(4−3y4))=1+4y4+y42=c0,4+c1,4y4+c2,4y42
prover 需要把多项式s4(y4)的commitment发送给verifier,也就是把该多项式的4个系数的commitment 之后发过去:
δc0,4=commit(c0,4)=commit(1)δc1,4=commit(c1,4)=commit(4)δc2,4=commit(c2,4)=commit(1)δc3,4=commit(c3,4)=commit(0)
verifier 需要验证:
s4(0)+s4(1)=?s3(2)=2
根据commitment 加法同态的性质,需要验证:
2δc0,4+δc1,4+δc2,4+δc3,4=?commit(s3(2))=commit(2)✓
验证通过,verfier 发送challenge factor r4=y4=4给prover,下一个round 需要验证的目标值为:
s4(4)=1+16+16=33mod5=3
基于y1=3,y2=4,y3=2,y4=4,prover 计算本次round 验证需要用到的proof,也就是单变量多项式s5(y5):
−−f(y5)8⋅−64y5⋅(18∗(26y5−34))+8⋅27y5⋅(18+(26y5−34))
则:
s5(y5)=8⋅−64y5⋅(18∗(26y5−34))+8⋅27y5⋅(18+(26y5−34))=3y5=c1,5y5
prover 需要把多项式s5(y5) 的commitment发送给verifier,也就是把该多项式的4个系数的commitment 之后发过去:
δc0,5=commit(c0,5)=commit(0)δc1,5=commit(c1,5)=commit(3)δc2,5=commit(c2,5)=commit(0)δc3,5=commit(c3,5)=commit(0)
verifier 需要验证:
s5(0)+s5(1)=?s4(4)=3
根据commitment 加法同态的性质,需要验证:
2δc0,5+δc1,5+δc2,5+δc3,5=?commit(s4(4))=commit(3)✓
验证通过,verfier 发送challenge factorr5=y5=1给prover,下一个round 需要验证的目标值为:
s5(1)=3
目前challenge factor 的组合为:
(3,(4,2),(4,1))=(y1,(y2,y3),(y4,y5))=(r′,rL,rR)
prover 根据第1层电路的evaluation 值很容易就能插值出相应的MLE 多项式:
V1(x1,x2,x3)=(1−x1)⋅[(1−x2)(1−x3)+4(1−x2)x3+2x2(1−x3)+x2x3]+x1⋅[4(1−x2)(1−x3)+4(1−x2)x3+x2(1−x3)+x2x3]
prover 分别计算出三个claims 值的commitment:
XYZ=commit(V1(r′,rL))=commit(V1(3,(4,2)))=commit(3)=commit(V1(r′,rR))=commit(V1(3,(4,1)))=commit(2)=commit(V1(r′,rL)⋅V1(r′,rR))=commit(3∗2)=commit(1)
verifier 拿着这三个commitment 完成第1层电路 sumcheck 协议的最后验证:
eq1(2,r′)⋅[mul1(4,hL,hR)⋅commit(V1(r′,hL)⋅V1(r′,hR))+add1(4,hL,hR)⋅(commit(V1(r′,hL))+commit(V1(r′,hR)))]=8⋅[−64∗commit(1)+27∗(commit(3)+commit(2))]=?commit(s5(1))=commit(3)✓
第一层电路evaluation 对应的MLE :
V1(x1,x2,x3)=(1−x1)⋅[(1−x2)(1−x3)+4⋅(1−x2)x3+2⋅x2(1−x3)+x2x3]+x1⋅[4⋅(1−x2)(1−x3)+4⋅(1−x2)x3+x2(1−x3)+x2x3]
上一个sumcheck 协议的Last Round中prover 新增加了两个claims,也就是:
V1(r′,rL)=V1(3,(4,2))=3V1(r′,rR)=V1(3,(4,1))=2
引入一个fold factor t 我们可以把两个claims fold到一起:
fH(t)=V1(r′,(1−t)⋅rL+t⋅rR)=V1(3,(4,2−t))=18−26t=3+4t
它的非常重要的特性就是:
fH(0)=3=V1(r′,rL)fH(1)=2=V1(r′,rR)
prover 把多项式fH(t)进行commit后发送给verifier,同样也是多个系数分别commit,该多项式degree 为2,也就是说最多有3个commitment:
δf0=commit(3)δf1=commit(4)δf2=commit(0)
verifier 拿到多项式fH(t)的commitment 后就可以计算出:
commit(fH(0))commit(fH(1))=δf0=δf0+δf1
这样就可以验证prover 之前发送的V1(r′,rL)、V1(r′,rR)的commitment 是否与当前多项式的commitment 是否一致:
commit(V1(r′,rL))commit(V1(r′,rR))=commit(3)=?commit(fH(0))=δf0✓=commit(2)=?commit(fH(1))=δf0+δf1✓
为了验证prover 之前发送的V1(r′,rL)、V1(r′,rR)的commitment X、Y是否合法,基于多项式fH(t)的commitment δf0、δf1、δf2, verifier 随机采样一个challenge factor v 并发送给prover,prover 自然可以计算出下一轮sumcheck协议需要证明的evaluation值fH(v),即:
V1(q′,q)=h′∈{0,1}bN∑hL∈{0,1}bG∑hR∈{0,1}bG∑Pq′,q,2(h′,hL,hR)=h′∈{0,1}bN∑hL∈{0,1}bG∑hR∈{0,1}bG∑eq2(q′,h′)⋅[mul1(q,hL,hR)(V2(h′,hL)∗V2(h′,hR))+add2(q,hL,hR)(V1(h′,hL)+V2(h′,hR))]=?fH(v)=3+4v
同时verifier 计算下一轮sumcheck协议需要证明的fH(v) 的commitment:
commit(fH(v))=δf0+δf1⋅v+δf2⋅v2
最后我们再明确一点:mini-protocol 的根本目的是把两个claims fold成一个claims,减少prover 的成本,不然prover要分别证明两个claims:
commit(V1(3,(4,2−v)))=?δf0+δf1⋅v+δf2⋅v2ORcommit(V1(3,(4,2))=?commit(3)commit(V1(3,(4,1))=?commit(2)
这样应该能make sense!
同Step TWO 一样,这里我们省略掉N 行文字+公式… 直接进入到Final Step!
我们再回顾一下最开始的实例结构图:
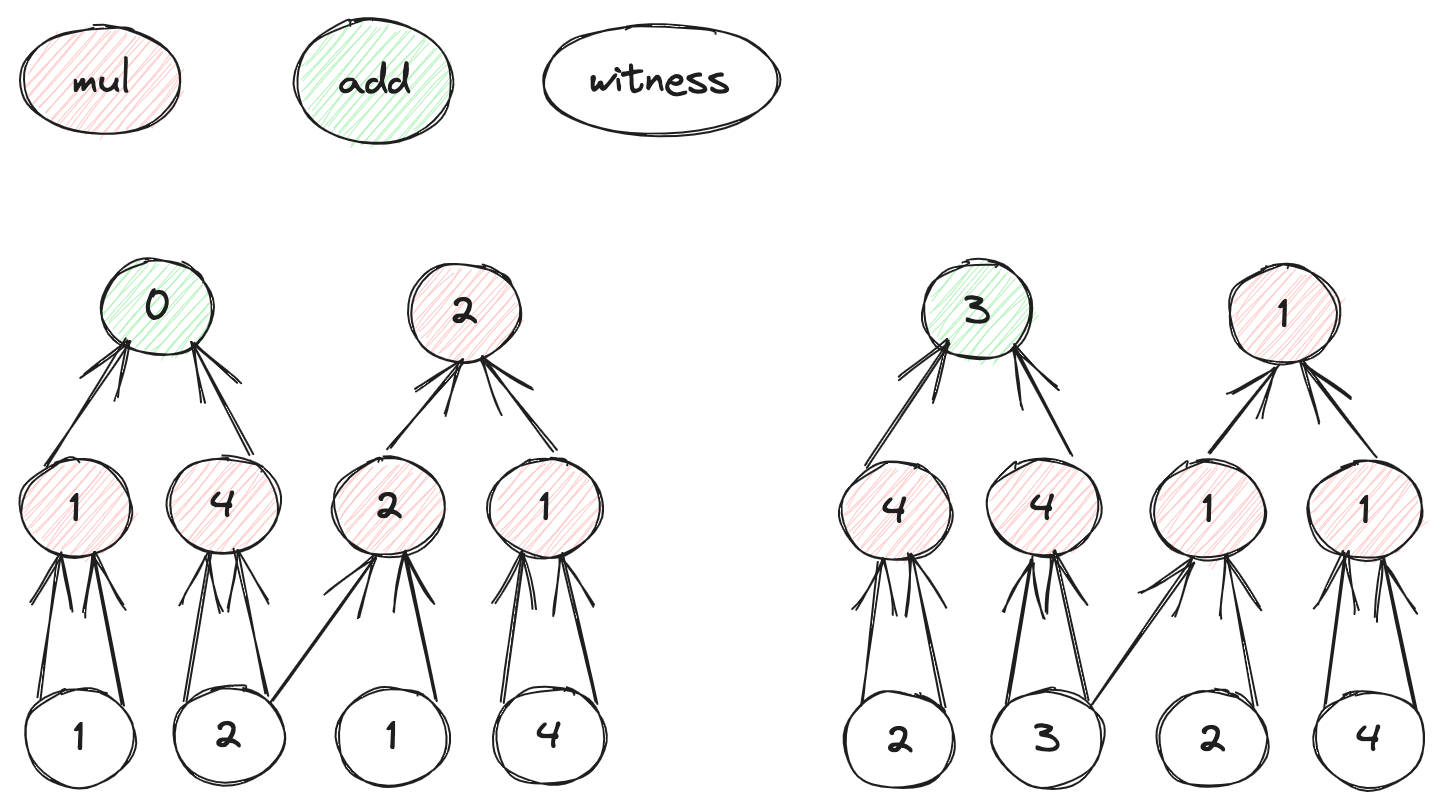
根据最下面一层(public input + witness)的值,我们可以插值出MLE:
V2(x1,x2,x3)=(1−x1)⋅[(1−x2)(1−x3)+2⋅(1−x2)x3+x2(1−x3)+4⋅x2x3]+x1⋅[2⋅(1−x2)(1−x3)+3⋅(1−x2)x3+2⋅x2(1−x3)+4⋅x2x3]
Step THREE 的mini-protocol 同样也会归结到证明两个claims,为了方便描述我们假设 (r′,rL,rR)=(2,(3,2),(3,3)):
V2(r′,rL)=?V2(2,(3,2))=0V2(r′,rR)=?V2(2,(3,3))=1
多项式fH(t):
fH(t)=t
假设fold factor v=2,把上面的两个claims合并成一个claim:
V2(2,(3,4))=?fH(v)=2
备注:简单一句话就是,证明最下面一层(public input+witness)电路、Gate编码为(2, (3, 4)), evaluation 值为2 ,组成的点在MLE 多项式上。
同样,verifier 基于prover 提供的fH(t)的commitment,计算出fH(v) 的commitment:
commit(fH(2))=δf0+δf1⋅2+δf2⋅22=commit(1)⋅2
verifier 如何验证prover 提供的这个commitment的合法性?对于verifier 来说最下面一层电路的evaluation 分 public input p和 witness w,其中后者未知,假设两者长度相等,按照上图中的实例,也就是说前半部分为public input,后半部分为witness:
(public input1,2,1,4,witness2,3,2,4)
因此,我们需要把V2拆解成两部分
V2(x1,x2,x3)=(1−x1)⋅p(x2,x3)+x1⋅w(x2,x3)
最终是要计算出V2(2,(3,4))的commitment,其中public input 部分因为是公开的,所以verifier 可以自行计算出相应的MLE 多项式p(x2,x3),并拿到p(3,4)的commitment;另外witness 部分因为在Step ZERO prover 已经把它们的commitment 全部都已经发给verifier 了,verifier 只需要基于此拿到w(x2,x3) 的commitment就可以了:
w(x2,x3)commit(w(x2,x3))=2⋅(1−x2)(1−x3)+3⋅(1−x2)x3+2⋅x2(1−x3)+4⋅x2x3⇓=commit(2)⋅(1−x2)(1−x3)+commit(3)⋅(1−x2)x3+commit(2)⋅x2(1−x3)+commit(4)⋅x2x3
最后的最后,我们put it together :
2⋅commit(1)=?(1−2)⋅commit(p(3,4))+2⋅commit(w(3,4))=4⋅commit(p(3,4))+2⋅[commit(2)⋅1+commit(3)⋅2+commit(2)⋅1+commit(4)⋅2]
到此为止,满足ZK argument的Vallina 版本的GKR协议也就完整了,紧接着我们再detail一下Hyrax 在此基础之上都做了些什么?接着再看看Spark 在Hyrax基础之上做了些什么?最后再看看Spartan 的整个全貌?
【1】Hyrax 论文:https://eprint.iacr.org/2017/1132.pdf
【2】PAZK by Thaler:https://people.cs.georgetown.edu/jthaler/ProofsArgsAndZK.pdf
【3】trivial GKR 协议:https://learnblockchain.cn/article/6199
【4】sumcheck 协议:https://learnblockchain.cn/article/6188





